Introduction to Quasicrystals
My original essay on "A 3-D Quasicrystal Structure?" now forms the core of this expanded note. Over time various additions and updates have set it in a wider context and morphed it into this more general discussion.
Some apparently crystalline structures have all the repeating local properties of a crystalline structure, yet overall they have no regular periodic pattern or translation unit. They are said to be quasiperiodic, and three-dimensional examples are called quasicrystals. Until recently their structure has been a mystery.
Quasiperiodic tilings of the plane
The Penrose tilings are well known quasiperiodic tilings of the plane. The most basic tiles comprise two kinds of rhombs, sharp and blunt, to which are added extra rules about how they may be combined. Without these rules, the rhombs could be arranged in many different periodic tilings.
Steinhard and Tsai found a two-dimensional quasiperiodic structure in the layered crystals of a particular Al72Ni20Co8 alloy. They have shown that it comprises overlapping decagonal atomic clusters.
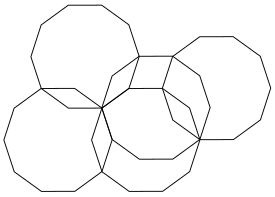
The overlapping pattern of the decagons appears to be closely related to the Penrose tiling. However the key to unlocking Steinhard and Tsai's structure is that many overlapping decagon tilings are possible but not all can be aligned with (or superimposed on) the Penrose tiling, and theirs is just such a non-aligned tiling.
A 3-D Quasicrystal Structure?
As far as I know this principle has not yet been extended to three dimensions, and no fully 3-D natural quasicrystal structure has yet been resolved. What follows is my investigations into this issue.
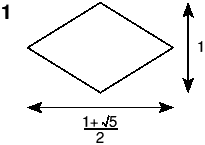
There is at least one promising candidate for just such a 3-D solution, which is summarised in the figures. Six root 5 rhombs (1) can form either of two rhombic hexahedra (or rhombic parallelepipeds); a flattened, oblate one or a sharp, prolate one (2).
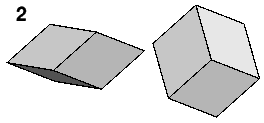
Two of each type of hexahedron (3) form Bilinski's rhombic dodecahedron (4). This dodecahedron fills space - though its packing is periodic, it demonstrates that the various solid angles of the hexahedra can combine to form closed vertices, a necessary precondition for space filling.
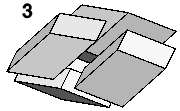
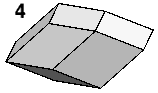
Three more of each hexahedron pack round the rhombic dodecahedron (5) to form the rhombic icosahedron (6), around which five more of each (not shown) pack to form the rhombic triacontahedron (7).
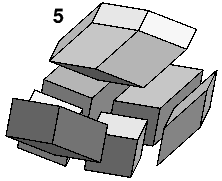
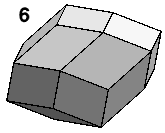
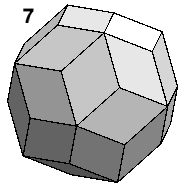
The two rhombic hexahedra are analogous to the two Penrose tiles, and the rhombic triacontahedron to a decagon formed from Penrose tiles. The decagons formed by a Penrose tiling are larger than the decagons of the underlying quasicrystal, so one could expect a similar relationship in any 3-D analogue. In the 2-D quasicrystal, the intersection of two overlapping decagons can also be formed from Penrose tiles. It is also possible to find an intersection of two rhombic triacontahedra formed from rhombic hexahedra. The analogous geometric principles are that all the 2-D polygons are parallel sided (zonogons), and all the 3-D polyhedra are parallel edged (zonohedra). The analogies are so close that the 3-D tiling is sometimes called the 3-D Penrose tiling.
Tilings and the dimpled rhombic triacontahedron
A spacefilling solid may be obtained by taking a conventional one and dimpling in triplets of faces. Each triplet is surrounded by a skew hexagon and eight such triplets may be found, corresponding to the eight corners of a cube. Forming a dimple requires the triplet to be rotated 60 deg. so that the skew edges remain attached to the hexagonal rim. Another way of understanding it is as a conventional rhombic triacontahedron with an oblate hexahedron scooped out.
If four of the triplets are dimpled, alternating around the triacontahedron with tetrahedral symmetry, the resulting solid is a conventional spacefiller Despite being a rhombic triacontahedron, this spacefilling is not quasiperiodic but fully periodic, with a cubic periodicity. It illustrates that, like the Penrose tiles, additional rules are required in how the subunits may be combined if a quasiperiodic structure is to be obtained.
This spacefilling can also be seen as conventional rhombic triacontahedra overlapping with four neighbours in a periodic tiling. I do not know whether quasiperiodic tilings of overlapping rhombic triacontahedra exist, whether 'non-Penrose' variants exist, and ultimately whether there exist real quasicrystals with such a structure - or even whether fully-3D quasicrystals are necessarily non-Penrose.
Some further reading is given in the References below. I do not have the resources to follow them all up, but would be glad to hear from anyone who does.
References
Thanks to Alex Day and Kate Crennell for many of these.
- British Crystallographic Association.
- Hargittai, I; "The Story of Quasicrystals", Chemical Intelligencer 3(4). (1997). p 25-29.
- Hart, George W; Encyclopaedia of polyhedra, Dissection of the rhombic triacontahedron (http://www.georgehart.com/virtual-polyhedra/dissection-rt.html).
- Kowalewski, Gerhard; Der Keplersche Korper und andere Bauspiele, Koehlers, Leipzig. 1938. Shows how to dissect a five-coloured rhombic triacontahedron into twenty three-coloured rhombic hexahedra (rhombic parallelepipeds). (In German)
- Mackay, A; Physica, 114A, 1982. p 609-613. Extends the Penrose pattern into 3 dimensions.
- David Nelson; "Quasicrystals," Scientific American, Aug 1986. pp 43-57.
- Schectman, D et al; Phys Rev Letters, 53, 1984. p 1951-1953. Discovery of a solid which extends the Penrose pattern into 3 dimensions.
- Joshua ES Socolar, Paul J Steinhardt and Dov Levine; "Quasicrystals with arbitrary orientational symmetry," Physical Review B, vol. 32 No. 8, pp 5547-5550, 15 Oct 1985.
- Paul Joseph Steinhardt; "Quasicrystals," American Scientist, vol 74, pp 586-597, Nov-Dec 1986.
- (re.) Sterinhard and Tsai; New Scientist, 27 February 1997.
- US patent No 5603188, "Architectural Body Having a Quasicrystal Structure".
Updated 27 Dec 2022