In search of the lost icosahedra
Updated 7 May 2023
This article is substantially reproduced by kind permission from:
Inchbald, G.; The Mathematical Gazette 86, July 2002, p.p. 208-215.
A few small corrections have been made:
- Miller was a fellow student, not their tutor.
- g1 comprises, specifically, 30 bipyramids.
- Face diagram 11 12 comprises nine parts, not six.
- Other minor typos.
Introduction
Just over sixty years ago Coxeter, Du Val, Flather and Petrie wrote The fifty-nine icosahedra. A new edition, with redrawn illustrations and useful additional material, has recently been published [1], making this a convenient moment to see if there is anything new to say. Coxeter once described the work as reflecting a certain 'youthful exuberance,' so do not be too surprised at what we find.
Stellations of a polyhedron are obtained by extending some of its edges or faces until they intersect at a distance from the original polyhedron. One way of studying stellations is to consider the planes in which the faces of the polyhedron lie, that is, its face planes. The face planes of the regular icosahedron intersect eachother (see Appendix) to dissect space into numerous regions, of which 473 are finite cells. These cells come in just 12 shapes which form layers around the original icosahedron, itself the innermost cell. The set of cells of a given shape comprises part or all of a layer, with icosahedral symmetry. The various stellations can be obtained by selecting different combinations of these cell sets. Because there are 12 types of cell and we are not interested in the 'empty' combination, there are 212 - 1 = 4,095 possible combinations.
To distinguish apart the combinations, and hence also the stellations, Du Val developed a symbolic notation based on the cells present: I use Du Val's notation here. I will also occasionally borrow the habit of referring to a stellation of the regular icosahedron simply as an icosahedron.
The 59 icosahedra
Many of the 4,095 combinations do not qualify as stellations, for various reasons. The fifty-nine icosahedra (I will tend to refer to it simply as The 59) sought to identify and enumerate the stellations. To give some guidance to the investigators, their colleague JCP Miller proposed five rules:
(i) The faces must lie in twenty planes, viz., the bounding planes of the regular icosahedron.
(ii) All parts composing the faces must be the same in each plane, although they may be quite disconnected.
(iii) The parts included in any one plane must have trigonal symmetry, with or without reflection. This secures icosahedral symmetry for the whole solid.
(iv) The parts included in any plane must all be 'accessible' in the completed solid (i.e. they must be on the 'outside'. In certain cases we should require models of enormous size in order to see all the outside. With a model of ordinary size, some parts of the 'outside' could only be explored by a crawling insect).
(v) We exclude from consideration cases where the parts can be divided into two sets, each giving a solid with as much symmetry as the whole figure. But we allow the combination of an enantiomorphous pair having no common part (which actually occurs in just one case).
Rules (i) to (iii) together secure icosahedral symmetry for the stellation. (iv) excludes any combination having one or more fully enclosed cavities, so ensuring that every stellation has a unique outward appearance. Lastly (v) forbids disconnected concentric compounds of simpler stellations: The 59 interpreted it as also forbidding vertex-connected or edge-connected concentric compounds, though the rule as stated is ambiguous. Application of these rules led to the enumeration of 58 stellations which together with the original icosahedron make up the 59 icosahedra described.
Some of the resulting stellations are evidently unsatisfactory. In particlular f2, shown in Figure 1, comprises twelve quite disconnected trapezohedra floating in space. As a loose collection of polyhedra it would appear to go against the spirit, if not the letter, of rule (v) which attempted to ban compounds of separate parts. g1 (Figure 2) is a collection of thirty bipyramids; they are at least vertex-connected but essentially the same criticism applies.
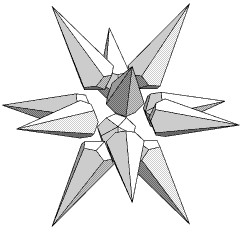 Figure 1 f2 |
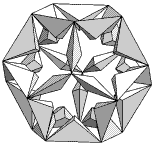 Figure 2 g1 |
Wheeler [2] had earlier discovered f2 and g1, listing them as 21 and 22 respectively, and he regarded them as being 'discrete' in form. All stellations identified before Wheeler were single polyhedra (or regular compounds) and the core polyhedron was always present. There is no doubt that the beauty and relationships of some hollow icosahedra make them worthy of study, though how can one stellate an icosahedron that is not there? Perhaps we should call them coronae, after the Sun's corona. How then did they get included in The 59, and did any worthy but as yet undiscovered stellations get left out?
To answer the first half of this question we need to see how The 59 approached the idea of a polyhedron.
Solids and faces
As a mathematical object a polyhedron can be approached as a solid block of space, or as a collection of faces, edges, or points (vertices). The same collection of edges or of vertices can be shared by several polyhedra of differing external appearance, so these approaches are not helpful here. The choice between faces or solid space is less obvious but there is an important difference in that a solid block of space has no internal structure. The importance of internal structure has been pointed out by Cromwell [3] among others.
The great icosahedron is stellation G. The associated face diagram 11 12 in The 59 (Figure 3) comprises nine irregular-shaped, discontinuous parts remaining wholly external to the solid. From it we can construct the vertex figure (Figure 4) (The vertex figure can be loosely thought of as the polygon exposed when a corner of the polyhedron is sliced off) which is seen to be incorrect: when Coxeter later co-authored [4] he gave the correct vertex figure (Figure 5), for the polyhedron 5/2 | 2 3. These figures illustrate how The 59 approached the icosahedra as solids and was not concerned with internal structure. As a consequence the term 'face' changed in meaning: the great icosahedron was originally named after the twenty triangular faces passing through its interior, leading Schläfli to give it the symbol 3, 5/2, which does not follow if the term 'face' refers to the irregular external regions of a solid form, as in 11 12.
 Figure 3 Face diagram 11 12 |
 Figure 4 Vertex figure of 11 12 |
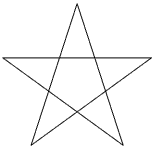 Figure 5 Vertex figure of 5/2 | 2 3 |
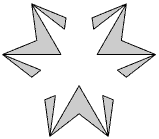 Figure 6 Face diagram 7 9 10 |
Face diagram 7 9 10 consists of three disconnected m-shaped groups of regions (Figure 6). It is not possible to tell directly whether the centre of the stellation is solid or hollowed out: in fact it is the regular compound of ten tetrahedra. The inclusion of internal structure is forbidden by Rule (iv), which is now seen to result in incorrect face diagrams.
Rule (ii) has a proviso that the parts of a face 'may be quite disconnected.' This has no relevance to the main purpose of the rule, which is to secure icosahedral symmetry. The proviso was added because, with no consideration of internal structure possible, it would have been unacceptable to exclude face diagrams such as 7 9 10. As a result, oddities such as g1 , f2 and others were able to slip through alongside the compound of ten tetrahedra.
Two lost icosahedra
Now we turn to the question as to whether any acceptable stellations might have been missed from The 59. Consider De1f1f2 (Figure 7). (In this and subsequent face diagrams, regions of the face seen from 'underneath' are shaded medium and interior regions of the face plane are shaded dark.) It can be obtained directly by extending the faces of the regular icosahedron and has no interior cavities or other questionable features, so it is a true stellation. Though it is not a compound in any accepted sense, rule (v) divides it into two stellations, De1f1 and the dubious f2 , which are connected only by their edges, and so excludes it from The 59. It is indeed a lost stellation, as also is its enantiomorph, De1f1 , since it lacks reflective symmetry.
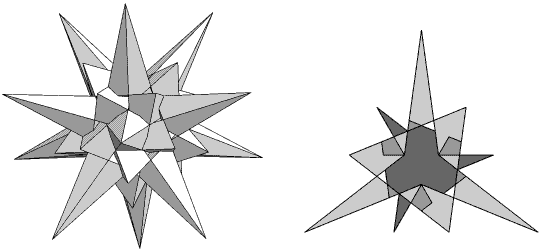
Figure 7
De1f1f2
Closely related to these are De1f1f2g1 (Figure 8) and De1f1f2g1 to which similar arguments apply.
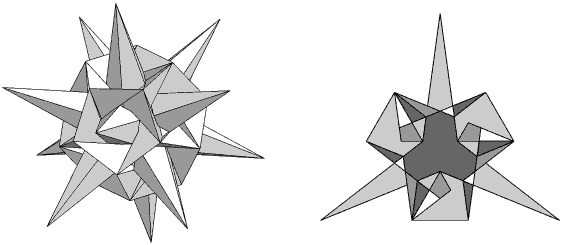
Figure 8
De1f1f2g1
Searching for alternative rules
We have seen that the original rules led to unacceptable consequences due to their failure to recognise the internal structure of a polyhedron, in turn a consequence of the approach to polyhedra as solids rather than collections of faces. Bearing in mind that the rules were originally proposed with no clear idea of the outcome, they are well overdue for revision.
Adherence to rules (i) to (iii) is necessary to secure icosahedral symmetry. We will want to be able to approach the icosahedra as collections of faces, so we should make explicit a fundamental rule which is assumed in The 59 (which approached polyhedra as finite solids), namely, 'The faces must close around a finite region of space.' These four rules could probably be simplified using Group theory.
Beyond this point answering the question, 'What are the defining characteristics of a stellation?' is not much easier than it was sixty years ago. I wrote a computer program to investigate some possible new rules in place of (iv), (v) and the proviso in (ii). The investigation was not systematic. Adherence to the five rules given above was achieved by ad hoc coding as required at the time: the code has not been validated beyond its ability to reproduce The 59 from Miller's rules, so its results can only be taken as indicative. While none of the new rules proved entirely satisfactory they yielded some interesting insights.
Starting from the definition of a stellation given at the beginning of this essay, I tried supplementing rules (iv) and (v) with 'All cells must be connected to another,' which negates the proviso of (ii), and 'The central icosahedron must be present (for if it is absent, it cannot be stellated).' These produced rather limited subsets of The 59.
Again from the definition of a stellation, we know that the properties of faces and edges are important. I suspected that the connectedness of the edges and/or faces is more fundamental that the connectedness of shells, so I tried substituting for rule (v), 'The faces must be continuous through the body of the icosahedron.' Although the total of 36 icosahedra allowed was still rather limiting, this found the two lost icosahedra described above and so confirmed the importance of the faces.
Next I investigated, 'All edges must be continuous through the body of the icosahedron, i.e. no separated collinear segments are allowed.' This again was less than a full answer while finding some interesting icosahedra; two are discussed here. Each face of acdf2g1 (Figure 9) is bounded by a single 15-sided polygon. It has the same external form as Df2g1 . Each face of be2 (Figure 10) is bounded by three overlapping rhombs (In passing, this figure helps to illustrate that the 'filled-in' form De2 is a compound of ten rhombic hexahedra, a property which I have not seen noted elsewhere.) Both these stellations fail rules (iv) and (v), but cannot be modified without destroying the bounding edges and/or the density rule of the faces (discussed below). Are these two more lost icosahedra?
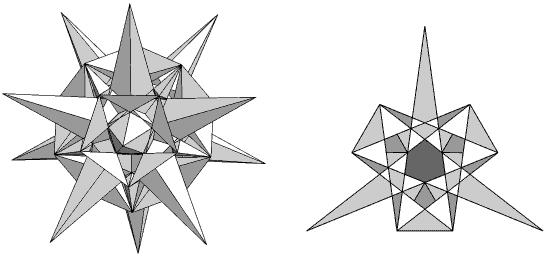
Figure 9
acdf2g1
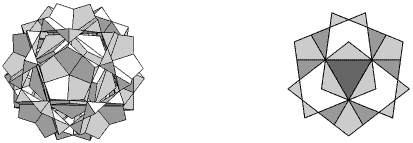
Figure 10
be2
The obvious next step was to explore an equivalent continuity rule for faces which would, in the language of The 59, be something like, 'The bounding edges in any one plane must form a single circuit or set of overlapping circuits about the centre.' In seeking to code this rule I found I had to consider the density of certain regions, especially the 'empty' inner regions, of the polygons and the fundamental question arose, what is a polygon? More specifically, can a star polygon be part 'filled-in' and part 'empty' and what rules apply - for example is the face diagram in Figure 9 a polygon? For a star polygon the density of a given region is the number of times the region is covered by a ray OP joining the centre of the region O to a point P as P makes a circuit round the edges of the polygon. The region outside has density equal to 0 and all regions inside have density greater than or equal to 1. For our purposes, we will think of regions with density greater than or equal to 1 as filled-in, and regions with density equal to 0 as empty. Referring to the star polygon in Figure 5 again, the pentagonal region in the centre has density equal to 2. But it also has density congruent to 0 (Mod 2), i.e. counting the density modulo 2 the star would have an empty, or hollow, centre. The density of the face diagrams in Figures 9 and 10 is also 1 modulo 2. Are these valid polygons? And is there any value in counting the density modulo 3, 4 and so on? Modular arithmetic would allow a more rigorous investigation of stellations whose faces are partially filled-in polygons, but I have not come across any previous work on such polygons: I would be grateful if any reader can point me to any suitable references.
Once we have a satisfactory definition of a 'polygon' for our purposes, we can go on to re-examine the principle of stellation, which should in turn lead to a better set of rules and a new enumeration of the icosahedra (and stellations of other polyhedra, too). We will want to recognise which regions of face planes, in the interior of the polyhedron, are filled-in and which are empty. Finally, we may have to ask whether there is a single 'right' principle of stellation to be found or to what extent it might depend on one's interests at the time.
Appendix
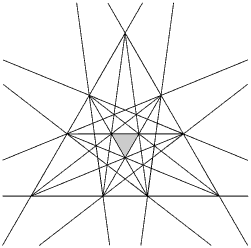
A face plane of the icosahedron is shown, giving the 18 lines of intersection with other face planes (one plane is parallel and does not intersect). The face of the original icosahedron is shown shaded.
Acknowledgements
The illustrations were created with the help of !Stellate software for RISC OS computers, from Fortran Friends, PO Box 64, Didcot, Oxon. OX11 0TH.
Printouts
The variations in Miller's rules were investigated on a computer using an ad hoc coded program. Its results cannot be guaranteed but I am not aware of any errors. The lists of stellations according to these variations are given a series of Program Printouts.
Postscript
Since writing the above article, it has occurred to me that the rules for finding stellations will be paralleled by equivalent rules for the duals of the stellations.
Every polyhedron has a dual or reciprocal polyhedron (obtained by reciprocating the polyhedron with respect to a sphere). For example the vertices of a uniform polyhedron (e.g. an Archimedean polyhedron) are equidistant from its centre, while the faces of its dual are similarly equidistant. Certain rules will define the relationship between polyhedra within a whole family of shapes, and reciprocal rules will define the reciprocal relationship within the family of duals.
The rules governing the duals of the stellated icosahedra, and their reciprocal relationship to the rules governing the stellations themselves, need to be investigated in parallel with the stellation rules, as through duality they effectively become a single topic.
References
- H. S. M. Coxeter (et al), The fifty-nine icosahedra, 3rd Edition, Tarquin (1999).
- A. H. Wheeler, Certain forms of the icosahedron and a method for deriving and designating higher polyhedra, Proc. Internat. Math. Congress, Toronto, 1924, Vol. 1, pp 701-708.
- P. Cromwell, Polyhedra, CUP pbk. (1999).
- H. S. M. Coxeter (et al), Uniform polyhedra, Phil. Trans. 246 A (1954) pp. 401-450.
Afterword
This was the initial investigation wehich set me off on the road which led to my theory of morphic polytopes. For a conceptual summary of that road, see It's a Long Way to the Stars. For the main waypoints along it, see mly lists of pages on stellation and facetting and on the general theory of polytopes and polyhedra.