Dualising Polyhedra
Updated 10 Feb 2024
The understanding offered here has developed piecemeal over a quarter of a century or more. The final analysys only became articulate after this note was first posted on the last day of 2022. It is, perhaps, the last chapter in my revisit to the general theory of polyhedra, building as it does on all the others.
In getting to this point, I should like to acknowledge the help and encouragement of many polyhedronists over the years, especially Paul Gailiunas, Branko Grünbaum, Norman Johnson and John Sharp. Sadly, many of them are no longer with us.
Contents
- Notions of duality
- Convex Euclidean polyhedra
- Topological or graph duality
- Projective dualities
- Abstract duality
- Standard and canonical duals
- Morphic duality
- Breaking reciprocity
- Vertex figures
- Conclusion
- References
Notions of duality
The way in which polyhedra team up as dual pairs, exchanging faces for vertices and vice versa, has been remarked on since antiquity. The cube has six faces and eight vertices, the octahedron eight faces and six vertices, both have twelve edges. Many attempts have been made to state a general theory, often to try and justify the claim that "every polyhedron has a dual," but oddities and exceptions always creep in and no basis has proved wholly satisfactory. Only a few short studies have ever tried to address such difficulties, and have made only limited headway. The root of the problem has been that we have approached polyhedra from various different theoretical directions, with the fundamental question as to “what is a polyhedron?” remaining to this day a topic of endless debate and confusion. Each approach brings its own understanding of polyhedral duality, and these dualities are no more consistent with each other than the approaches themselves are. The phenomenon was noted by Gailiunas & Sharp (2005), but I give here a slightly different classification of the various approaches:
- – Convex and highly symmetrical solids
- – Graph connectivity and topological surfaces
- – Projective geometry, especially polar reciprocity
- – Combinatorial or abstract sets
These four approaches – convex, topological, projective and setted – have all proved to be incompatible with one another, at least as conventionally treated; the folklore attempts to stitch them together into a unified picture are badly broken (Grünbaum & Shephard 1988). The impact of all this on duality is what I shall be exploring here. Some of the root problems only manifest in higher-dimensional “polytopes” – generalisations of polyhedra in any number of dimensions. I will try to ensure that my discussion is consistent with polytopes in general, while avoiding such complications as far as possible.
Despite the apparent chaos, my studies have revealed deep connections and consistencies across certain aspects of the various approaches, with all of them required for a full understanding of polyhedra. Their relationships provide the mathematical foundation for my theory of morphic polytopes, and also have a profound impact on the mechanics of polyhedral dualities.
But before going any further, just what are these polyhedra we want to discuss? The term has been much bent or redefined, some may say abused, for the convenience of one theory or another over the years. Many incompatible definitions may be found across the literature, all applicable in their own sphere of interest. (Lakatos 1976)
Here, polygons and polyhedra are understood in their historic geometrical sense, as respectively two- and three-dimensional examples of the more general polytopes in any number of dimensions. A one-dimensional polytope is a ditelon (two-ended) or line segment. A zero-dimensional polytope is a monon (singleton) or point.
Broadly speaking, we can say that a ditelon is a closed segment of a 1-dimensional line. “Closed” in a geometric context means that it includes its two bounding points. In a polyhedron or polytope we call these points vertices and may treat them as monons. A polygon is, or is bounded by, a closed loop or circuit of ditela lying in a 2-dimensional surface. A polyhedron is, or is bounded by, a closed surface made up of polygons and lying in a 3-dimensional space. Crucially, just two ditela meet at each corner or vertex of a polygon, and just two polygons meet at each edge of a polyhedron. Similarly, just two polyhedra meet at each face of a polychoron, and so on. This is sometimes called the dyadic property.
This definition is not rigorous, nor even complete. For example I have not said whether or not polygons must be flat, nor whether the interior enclosed by the boundary is an integral part of the figure. Each theoretical approach brings its own definitions of such things. Several will be encountered below.
Duality too is a much misunderstood concept that bears some clarification. In a general sense it is not confined to polytopes but is a widely observed phenomenon. The Yin and Yang of Eastern philosophy, in which every aspect of an idea is reflected in its opposite, offer perhaps the earliest expression of its generality. Mathematical transformations offer many modern examples of dualities, such as the Fourier transform creating a duality between sound waveforms and their frequency spectra, or the ADS/CFT gauge/gravity duality of theoretical physics. Closer to home, there is a geometrical duality between the layout of a trussed girder and the diagram of forces within its members. So just because you find a duality in one theory of polyhedra, this does not mean that it is the same duality you found in another theory.
Among the many and varied dualities, those of particular relevance here are transformations which are their own inverse; applying the same transform to the dual recovers the original object. Familiar examples include reflection in a mirror, or the inversion or reciprocation of a number. All polyhedral dualities are of this type.
To construct a dual polyhedron we make its vertices into faces, and vice versa, and redraw the edges between them accordingly. But beyond that, the devil is in the detail. It is not always as easy or as clean as it looks. So the next thing to do is to take a look at each of the four approaches to polyhedra and their duality.
Convex Euclidean polyhedra

A square as the intersection of four half-planes.
The dual construction is not immediately obvious.
Duality was first noticed among the highly symmetrical Platonic figures; the cube is dual to the octahedron, the dodecahedron to the icosahedron, and the tetrahedron is self-dual. Euclid developed the theory of geometry which bears his name and constructed these polyhedra in his Elements, but for the next two thousand years their duality remained an unexplained mystery.
To Euclid, a polyhedron was a flat-faced solid which existed in the infinite, smooth and contiguous space which we name after him. Only convex examples were studied. That is to say, you could draw a line (segment) from any point in the solid to any other, and the whole of the line would lie within it. Every face was a convex polygon.
The most symmetrical forms, principally the regular convex or Platonic solids, have entranced geometers since the earliest times and spurred much of the early research. These symmetries lay at the heart of early observations of polyhedral dualities, and would continue to influence polyhedral thoughts and habits long after their independence from their associated polyhedra was established. Dualities became apparent within these symmetries, most evident in the construction recipes for the regular polyhedra, known as Schläfli symbols; {3 3} which is self-dual, {3 4} and {4 3}, and {3 5} and {5 3}.
For a given polyhedron, its dual was typically constructed by taking the centre point of each face, joining these points with new edges, and these edges with new faces, thus creating the dual inside the original. One might consider this an early form of constructing a Euclidean dual.
From the days of Descartes, it has become customary to apply x, y, z coordinates to Euclidean space and to analyse constructions in it accordingly. In this scheme, symmetries are represented by transformation matrices which convert one set of coordinates to another.
In recent times the idea has arisen of dividing space into two halves by the plane in which a face lies. The polyhedron lies inside one of the half-spaces and outside the other. We can then define the polyhedron as the region formed by the intersection of the “inside” half-spaces created by every face. This has become an extremely powerful general mathematical tool, embracing anything from the linear programming of mixing up optimal chemical or agricultural feedstocks to the calculation of particle interaction probabilities in the strange twistor space of high-energy physics.
Dualsing such a polyhedron, defined by half-spaces, is a laborious process which abandons the half-spaces as such and must instead use their bounding planes to derive suitable points and/or lines from which to construct a new set of half-spaces. In practice it may be easier to define the dual by its set of vertex points and then to construct its face planes. This also sits well with the idea of treating space as comprising all the points identifiable by their Cartesian coordinates.
The whole thing is still quite awkward. Only the most symmetrical or simple of polyhedra exhibit dualities which are immediately obvious. If you dualise a polyhedron, then dualise the dual using the same construction method, most such methods will not recover the original figure but one of a different size, perhaps even distorted in some way. There is no elegant general treatment within this mathematical model, which is perhaps why Cartesian coordinates remained the only significant advance for two thousand years. In the last few centuries geometers have found neater shortcuts, but they have had to turn to alternative mathematical treatments to do so.
Topological or graph duality

(Black) A graph equivalent to the cube.
(Red) The dual octahedral graph. The outer
region represents one face of the polyhedron.
It was not until 1750 that Leonhard Euler published his pioneering formula relating vertex, edge and face counts, V−E+F=2. He happened to be the first to study each of two distinct phenomena, the connectivity of planar graphs and the edges of convex polyhedra. His formula turned out to apply equally to both. This discovery signalled the birth of a new theoretical approach to topological structures such as graphs and complexes on manifolds. He called it Analysis situ but we know it better today as Topology.
Dualising a graph is easy enough. We mark a new vertex in each region of the graph, not forgetting the region outside it, and join pairs of adjacent vertices across the separating edge. Dualising a polyhedron or a graph turns out to exchange the values of V and F in the formula, leaving the result unchanged.
But not all polyhedra are convex and these others turned out to yield various alternative results for his formula. This Euler value χ proved to capture certain characteristics of the surface. For example all polyhedra with a hole in have χ=0. This presently gave rise to the discipline of topology, in which the structural form of the figure is of fundamental interest, while matters of size or proportion or position in space become irrelevant. The Euler value and other related properties came to be treated as the defining characteristics of a given topological form or manifold. Ultimately, a polyhedron could be treated as a graph drawn on some associated manifold. Since dualising a figure does not change these defining characteristics, the dual of a polyhedron is then just the dual graph drawn on the same manifold. [Grünbaum 2007]
For example any convex polyhedron corresponds to a planar graph, with the "outside" of the graph being counted as one of its faces. Topologically it is a sphere. In all these cases, χ = 2. However a graph drawn on say a torus, having χ = 0, cannot also be drawn on a plane.
In this sense any quadrilateral hexahedron, constructed with three faces at each vertex, is topologically equivalent to a cube; we say that they are all isomorphs. They are all topologically dual to any triangular octahedron which is isomorphic to the regular octahedron.
If we wish to establish any kind of dual correspondence between particular geometric figures, topological duality is a prerequisite. Indeed, it has become the defining principle of polyhedral duality in general. But on its own it is not sufficient to define a unique dual for any given geometric figure. For this, properties such as scale, proportion and position must be derived from some other geometrical principle.
Projective dualities
Projective duality and polar reciprocity
A quite distinct approach to duality appeared through the 19th century, with the development of projective geometry.
Edwards (2003) treats the subject in an unusual fashion, being synthetic and practical rather than analytic in tone – indeed you will find more philosophical remarks or construction procedures than equations in his book, which is none the less rigorous for that. I have found this approach to be particularly useful in encouraging the mindset required to follow through the ideas which I present here. The reader who struggles with this section may benefit similarly.
As the axiomatic form of projective geometry took shape (equivalent to Euclid's postulates), it established the well-known theorems of projective duality. For any construction of points and lines in the projective plane there is a dual construction of lines and points. You can even exchange any formal statement about points and lines with a dual statement about lines and points. Similarly in projective space one deals with points and planes.
If you apply some projective construction to a point, which transforms it to another point, and find that applying the same construction to the new point transforms it back again, then you have established a reciprocity between the two points.
An example is provided via the existence of a polarity in the plane about a conic curve. A circle is a convenient example of a conic. Any point has a corresponding polar line, and vice versa. Such a point is called a pole, and the line is its polar with respect to the given conic. Take any point on the polar, and its own polar will meet the original point. This sets up a polar reciprocity, in which the two poles and polars form a reciprocal pair. In three dimensions, such a polarity may be establiched about any quadric surface, usually a sphere. In this case the polar is a plane and a reciprocity may again be again established between poles and polars. Of significance here is the property of polar reciprocity, that it is an example of a projective dual construction.
Polarising polyhedra

Reciprocal arrangement of polygons Π and Π' about circle s.
It follows from the above that reciprocating any polyhedron about a concentric sphere constructs a projective dual – the dual polyhedron. Introductions to the polar construction of such reciprocal figures are given by Wenninger (1983) and Gailiunas and Sharp (2005).
The illustration shows the basic construction for reciprocating polygon Π about circle s. The pole K' of edge k is found by constructing tangents where it intersects the circle. The polar a' of vertex A is orthogonal to the ray OA. Working round the figure, the reciprocal polygon Π' is constructed.
Consider the basic case of a convex polygon. We often treat its interior as a set of points. Such a point may be identified by drawing a ray from the point to the polygonal boundary. We then rotate the ray about the point, such that its point of intersection with the boundary travels along it until, after a full turn, the point of intersection has completed a full circuit back to its starting position. Thus, the interior may be defined as the set of points about which the polygon winds.
Projectively, we may also treat the exterior plane as the set of lines which do not meet the polygon. When we polarise the polygon in a concentric circle, we find that the interior points polarise to the exterior lines of the dual polygon and the exterior lines to the interior points of the dual. The principle readily extends to polyhedra. Here, we treat the exterior space as a set of planes, and these turn out to be reciprocal to the interior points of the dual polyhedron. And so on in higher dimensions.
Consider now what I will call a polygonal curve, which is a smooth curve approximated by alternating vertices and line segments. If we walk along the point of intersection with the ray as we rotate it, then at each vertex we will turn through its external angle in order to continue along the curve. Around a convex polygon, the sum of the external angles is constant, i.e. 2π; if we were to assume internal angles, the sum would vary. It is therefore important to always take the exterior angles (although I hope to show later that this can create ambiguities).
Projectively we may treat a line segment as a dense set of points bounded by its two end points, and an angle as a dense set of rays bounded by the two lines which form it. When we reciprocate a polygonal curve about a conic, the points of the segments reciprocate to exterior angles. The dual of this is that the rays of the exterior angles reciprocate to the interior points of the line segment. It is all very neat and elegant.


Reciprocities between segment interiors and exterior angles. In general, x' is reciprocal to X and X' to x.
It is often said that this approach can be easily adapted to self-intersecting figures such as stars. Poinsot argued that the regular stars are convex anyway, because all their vertices are convex. Cayley developed the idea of interior density, according to how many times the boundary winds or wraps around any given interior point. Coxeter assumed it to be true. But for non-orientable polyhedra, one cannot establish anything more than a parity value for the density; Cayley's idea only works for orientable figures. As far as the reciprocity of inside and outside goes, the situation is even worse. For any star, indeed for any non-convex figure, we find that certain interior points reciprocate to lines which do meet the dual figure.
Projective manifolds and the Absolute
Closely associated with the fundamental nature of projective duality is the topology of projective spaces or manifolds. In projective geometry, every line in the plane meets every other line in just one point, while every plane in space meets every other plane in just one line. Unlike Euclidean geometry, it has no concept of parallelism, no “parallel postulate”. Euclid's idea that parallel lines never meet turns out to create a space almost identical to the projective, except that the place where these lines would have met in projective space must be ripped out of Euclid's. This removes a line from the projective plane, known as the Absolute line, and similarly an Absolute plane from projective space. They leave behind a yawning gap, a discontinuity which can fortunately never be encountered in Euclidean geometry because it lies "at infinity". There is no such gap in a projective space, which therefore wraps back on itself as an unbounded manifold. This gives projective and Euclidean geometries subtly different qualities.
There are many ways to map one manifold or space into another, for example we can map the infinite projective plane into a finite Euclidean circle via a stereographic projection. Why should we necessarily treat Euclidean space as the projective with a bit missing, and not the other way round? One sign in this direction is the nature of transformation matrices. Affine transformations turn out to be a subgroup of the projective, and Euclidean to be a subgroup of the affine. There are projective transformations which are not Euclidean, but there are no Euclidean transformations which are not also projective. A more rigorous demonstration may be found in the axiomatic definitions of these geometries. We can think of each axiom as restricting the scope of the geometry in some way, as restricting the range of valid constructions possible within the geometry. Euclidean geometry can be formulated simply by adding the parralel postulate to the axioms of projective geometry. Thus, with this extra axiom, Euclidean geometry is more restrictive than the projective.
Properties of the Absolute can sometimes be necessary in projective geometry. For example the polar of a circle's centre is the Absolute line, while that of a sphere's centre is the Absolute plane. Thus, the theorems of projective duality do not hold in Euclidean geometry and the construction of a projective polarity may not be possible. This is further discussed below.
Abstract duality
In the 20th century yet a fourth approach emerged. Set theory became fashionable in mathematics and geometers began reformulating space as a set of points. Different kinds of space led to different kinds of set. Euclidean space was a dense point set of infinite size. Finite-set spaces could be created by allowing only a finite number of points. Polyhedra were naturally treated likewise, and to keep them manageable only the vertex points were considered. An edge was treated as a point pair, a polygon as a set of such pairs and the polyhedron itself as a set of such sets of pairs. The combinatorics of these vertex point partially-ordered sets (posets) came under much scrutiny.
When dualising such a poset, what had been a vertex became, combinatorially, a cyclic set of cyclic point pairs, i.e. the cycle of faces around it, and vice versa. Consider for example a triangular prism having vertices ABCDEF. As a combinatorial set of points it might be depicted as something like the set of the following members:
A B C D E F
{AB} {BC} {CA} {AD} {BE} {CF} {DE} {EF} {FD}
{{AB} {BC} {CA}} {{AB} {BE} {ED} {DA}} {{BC} {CF} {FE} {EB}} {{CA} {AD} {DF} {FC}} {{DE} {EF} {FD}}
where the six sets representing faces, of multiple pairs of elements, are each cyclically ordered. Transforming such a combinatorial set of sets to obtain that of the dual trigonal dipyramid involves transforming each set of pairs to an atomic vertex point (say G, H, ...), and then each of A, B, ..., F to a set of pairs of those new points. It is clearly a nightmare, and was a nasty step backwards.
Eventually work on this, and a more general approach to incidence complexes comprising sets of points, line segments and plane regions, developed into the idea of an abstract polyhedron as a hierarchical set of elements, where each edge or face was treated as an element of the set in its own right.
In the study of incidence complexes, focus is laid on the connectivity of the various elements – vertices, edges, faces and so on – which make up the complex (such as a polyhedral surface). This pattern of connectivity may also be represented as a poset of members or elements, in which the elements are ranked by their dimension. In addition each element of intermediate rank is connected to certain elements of one dimension higher, and of one lower, by a binary or pairwise "incidence" relation.
A set diagram of any incidence complex may be constructed, in which the elements of a given rank lie horizontally aligned in a row, the ranks are ordered by dimension, and each incidence is drawn as a line connecting the two elements. This is known as its Hasse diagram.
For an incidence complex to comprise a polytope, certain rules apply. These include the dyadic property, which in this model is also known as the diamond condition after its characteristic appearance in the set diagram. Another curiosity of this set-theoretic basis is that a maximal element or body must be present, along with a minimal null polytope or nullon analogous to the empty set or the number zero. Such a poset is known as an abstract polyhedron or, more generally, an abstract polytope.
As I note in A Critique of Abstract Polytopes, at first the combinatorialists still treated each abstract element as a set of vertex points. However such an understanding turned out to be an unnecessary complication and the set theory of abstract polytopes is most elegantly expressed if each element is atomic, i.e. a fundamental object or "primitive" in its own right.
In order to construct a real geometric figure, the abstract polyhedron is “realized”, i.e. envisaged as being injected or mapped into some containing real space, usually Euclidean.
Now, here’s the killer. In order to obtain the dual of an abstract polytope, the order of ranking is simply reversed. Informally, one can regard this as turning the Hasse diagram upside down. That is all there is to it! It is a staggeringly economical and beautiful result, surely comparable to Euler's historic formula.
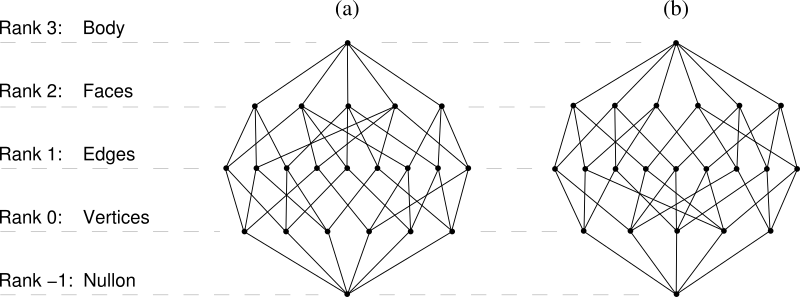
Hasse diagrams of; (a) the triangular prism, (b) its dual trigonal dipyramid
The diagrams are isomorphic but ranked in opposite directions (opposite ways up).
In a strong sense, both geometric dual figures share the same abstract structure, and choosing which of the dual pair to realize is just the choice of which direction to adopt for the ranking order.
This kind of duality was originally referred to as combinatorial duality. However it is very different from the combinatorics of point sets and abstract duality might be a better term. Moreover the atomic model of abstract polytopes as incidence structures lends itself to a powerful algebra all its own and, although a relatively recent development, the theory is evolving rapidly.
In Polytopes, Duality and Precursors I refer to the undirected abstract set as a precursor. This, together with its two dual realizations, forms an overall schema. This in turn may be compared to the only slightly longer-established understanding of cuboctahedral symmetry giving rise to the dual pair of cube {4 3} and octahedron {3 4}, with icosidodecahedral symmetry doing the same for {3 5} and {5 3}.
Standard and canonical duals
Given the four independent approaches to polyhedra and their duality just descrbed, we can now turn to the problem of forming a consistent theory across them all.
The duality of all geometric polyhedra, by which every polyhedron is twinned with a dual, or reciprocal, geometrical figure, has become a common tenet of mathematical folklore. In particular, the notion that we may reciprocate any polyhedron about a concentric sphere, and thus obtain a suitable dual, is so widespread that it defines what I will call the standard dual of any polyhedron. The standard dual may vary in size, according to the radius of the chosen sphere, but its geometry is otherwise fixed. The Dorman Luke construction is commonly used for uniform polyhedra.(Cundy & Rollett 1961)
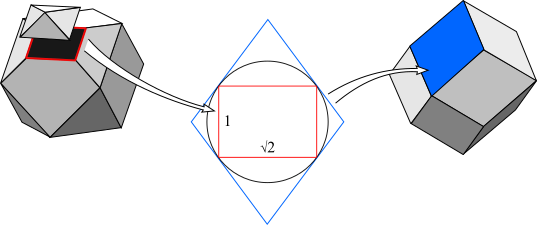
Dorman Luke construction for the rhombic dodecahedron,
showing the duality of vertex figure (red) and face (blue).
One manifestation in particular has been elevated to canonical status. Any given polyhedron which is a topological sphere (i.e. χ=2) can be morphed into a convex form which has an intersphere, tangent to all its edges, without changing its structure. This tangent solution for each polyhedral structure is unique and is known as its canonical form. The Platonics and Archimedeans are examples of such canonical forms. The polar reciprocal with respect to a common intersphere is then its canonical dual, and the whole arrangement forms a canonical dual pair. The Catalans or Archimedean duals are also canonical. The whole arrangement together with its common abstract poset might be regarded as a canonical schema.

Cuboctahedron (light) and rhombic
dodecahedron (dark) as a canonical dual pair.
Extending these ideas to less straightforward polyhedra begins to create problems. Studies exploring some of these issues include Wenninger (1983), Grünbaum & Shephard (1988) and Gailiunas & Sharp (2005).
Wenninger assumes central symmetry as given, and consequently runs into a conflict between the projective Absolute and Euclidean infinities when dualising the uniform hemipolyhedra, self-intersecting polyhedra which have faces passing through their centre of symmetry. In consequence his dual figures have vertices at infinity, a solution which he recognises as mathematically flawed and not strictly polyhedra any more.
Grünbaum & Shephard observe that much widespread understanding is no more than unproven folklore and often wrong. In particular, once away from the strict assumptions of convexity and symmetry, things can go awry. Had they accepted a wider view, allowing non-convexity and self-intersection, they acknowledge the effects they note would not have been problematic and the insoluble dilemmas would have found solutions. They feel the need to assume a convex mindset, noting the lack of any theory of self-intersection for topological models and looking forward to such a development.
Gailiunas & Sharp similarly bemoan the lack of either quality or quantity in the published literature. They again consider combinatorial duality in the context of planar graphs (i.e. convex polyhedra), and point out certain difficulties that arise with the early Euclidean process when less simple manifolds (i.e. χ≠2) are considered. They go on, via a useful exposition of polar reciprocity, to give examples of solutions which Grünbaum & Shephard did not allow themselves. Their examples amply demonstrate that, in the general case, neither local (non)convexity nor self-(non)intersection is preserved under polar reciprocity.
These short studies all share a common theme, that once convexity and symmetry are left behind, polar reciprocity renders our conventional Euclidean-based understanding hopelessly naive. However none of them offers any systematic understanding of the inconsistencies through which the various difficulties arise.
An example which they do not touch on may be found with the regular star polyhedra. These also form standard dual pairs which may, moreover, be constructed around a common intersphere, however they are not canonical in form; the canonical forms of the great stellated dodecahedron and great icosahedron are respectively just the regular convex dodecahedron and icosahedron, while the small stellated and great dodecahedra are not topological spheres and no canonical form is defined for such polyhedra.
At this point it is worth a quick recap of what this standard approach is actually doing. First of all, its aim is to construct the combinatorial or abstract dual of some original polyhedron, while preserving its overall surface topology. At the same time we wish faces to remain flat, edges straight, and symmetries in Euclidean space conserved. The chosen method is the projective polar reciprocation of the original about a concentric sphere.
So it is mashing together several different branches of mathematics, each with its own approach to polyhedra and to their duality, in the hope of achieving a consistent picture. Perhaps the most surprising thing, when expressed as it is here, is how far this endeavour can actually succeed with convex polyhedra. Less surprising on reflection is the number of difficulties which can arise in less straightforward circumstances, where the disparate fundamental assumptions of the various approaches create inconsistencies between then.
Morphic duals
In seeking a consistent understanding, it should now be clear that both what we take to be a “polygon” or a “polyhedron” and how we choose to “dualise” them have profound consequences. Further consideration of these issues leads on to revisiting our ideas of how to define a polyhedron, its inside and outside, and even of exactly what kind of space we wish to dualise our polyhedra in.
All this was part of my motivation for developing my theory of Morphic Polytopes, including morphic polyhedra. A morphic polyhedron may be understood as a graph drawn on some associated topological surface or manifold. It represents an intermediate stage in the realization of an abstract polyhedron as a geometric object, as an interpretation of the abstract elements as vertices, edges and faces ranked in a given order. The dual morphic polyhedron is then the same abstract set but interpreted in the reverse ranking order to yield the dual graph on the same manifold.
The second stage of realization is to concretize the polyhedron in some geometric space. If we then reciprocate it about a quadric such as a sphere, the reciprocal manifold will have the same topology as the original, while projective duality ensures that the abstract polyhedron is preserved, albeit realized with reverse ranking. Thus, the reciprocal figure is an example of the dual polyhedron. However if for example the destination space is badly chosen, then there is no guarantee that the dual polyhedron will fit inside it, and a degenerate geometrical figure may result.
The intermediate stage of morphic polytopes goes a long way towards meeting Grünbaum & Shephard's aspiration for a general theory of self-intersecting polyhedral manifolds. However the overall process does not guarantee that a concrete dual figure will be a faithful realization of the abstract polyhedron. Problems are especially likely to arise in Euclidean space.
The abstract formulation poses another difficulty in that it allows more general structures than does topological decomposition. Specifically, any given piece of a polytope need not be simple (a topological ball) but may have structural holes or twists in it (an example is offered by what are known as projective polytopes). Thus its structure, when drawn on the associated manifold, will not be a valid topological complex but will have non-simple (anaploid) pieces. The abstract and topological approaches turn out to be compatible only to the extent that topological polytopes comprise a subset of the abstract. This does not mean that the topological approach is broken or incomplete, rather that the standard tools of topological analyisis may not be applicable to all abstract polytopes.
So, does it mean that abstract theory is inappropriate, too general? Is it necessary to accept its anaploid pieces? Why not just leave them out and return to a topological definition, rejecting such figures as the projective polytopes, mentioned above, as true polytopes? In my discussion of Morphic Polytopes there are two chief reasons why not. The first is the simple elegance of abstract theory and the deep intractability of characterising anaploid polytopes. The second reason is exemplified in the hollow star pentagon which forms the vertex figure of the pentagonal cornoid. The body of this polygon is a Möbius band and hence is anaploid. Such figures crop up arbitarily in studies of many aspects, and to deny them complicates or ruins many a neat observation. This parallels the first reason; there are just too many anaploid polytopes out there for us to dismiss them so lightly.
The morphic approach offers a unified understanding, taking the abstract set as a basis, but adding the interior topology of each piece to complete the picture. Any inconsistencies are resolved at the interpretive level of realization. Any projective issues are handles at the concretizastion level. Thus it harmonises the topological, projective and abstract approaches to polyhedra and their duality. But, as we shall see, it only achieves this flawlessly where polar reciprocity is a consequence of a deep theorem, in other words in projective spaces.
Breaking reciprocity
We usually like to work in Euclidean space. It can be understood as a projective space with a Cartesian metric applied and the Absolute plane, polar to the coordinate origin, removed. As a direct consequence of this last, the projective duality of statements about points and planes no longer holds as a theorem.
For any arrangement which has an undercut, in which the outside of a face is oriented towards the centre of reciprocation, there will be at least one external angle which includes a line or plane incident on the centre. The pole of that line or plane is a vertex located at infinity. You can discover this for yourself if you attempt the construction, as illustrated above, with the circle centre located oustide the original polygon. Unfortunately, the Euclidean formalism has removed infinity from its geometry, so the construction cannot be carried out; you will end up with two parallel tangents which cannot converge on a pole. This applies not only to asymmetric situations where the centre of the sphere lies outside the polyhedron, but also in many other situations.
This phenomenon is not usually appreciated, as there is an unconscious trick we play which hides it from us. Like a sphere, the projective plane has no boundary and a line in it makes a closed loop around the surface. Similarly, any line in projective space forms a loop. However unlike a 3-sphere, any line not in a given plane must meet that plane exactly once. Thus, when we make the space Euclidean, every line extends across space but is broken where the plane at infinity has been ripped out. Given a finite line segment in Euclidean space, the line it is on extends in both directions; it has two infinite segments as well as the finite one. But if we return it to projective space, these two infinite segments rejoin and the line is divided into only two segments, of equal status.
Given the reciprocation of some arbitrary construction which results in one of these segments, it is equally arbitrary which one it will be. Thus, back in the Euclidean domain, our reciprocal figure might or might not suffer Wenninger's fate. In fact Wenninger's is a special case as it applies to the bounding line or plane of some angle, and this raises additional paradoxes all its own.
Wenninger's hemi polyhedra are a transitional case where a face lies on the line meeting the centre and different sides of the face have exterior angles on different sides of the face. Thus, the angles on both sides have bounding lines which meet the centre and therefore the pole lies at infinity in both directions. But that point at infinity is outside space, and so the polyhedral structure is irretrievably broken. If you move the centroid of the sphere a little so that it no longer lies in the face plane, then the vertex reappears at a finite distance and you can construct a finite dual in the usual way. However its symmetry is spoiled. In a projective space the structure is preserved throughout.
In practice we ignore all this and simply pick the finite segment for our dual polyhedron. The standard dual of an undercut polyhedron is not in fact its projective reciprocal, but a fudge fabricated through our own ignorance. So let us be more accurate and say that the standard dual is that figure which arises from a polar construction, where we choose the segments and faces which do not cross infinity.
We get away with the trick because the choice of segment does not affect the connectivity of the elements, and therefore leaves the abstract and topological forms intact. But we break strict projective reciprocity nonetheless.
It has already been noted how the inside and outside of a non-convex or asymmetric arrangement do not polarise in any useful way. Projective polarity is no help in choosing which region(s) of a plane to treat as inside or outside the dual figure.
Another problem arises if we wish to preserve the geometric symmetries of the original polyhedron. The polars of its edges and vertices extend equally in all available directions and it becomes entirely arbitrary which we choose for the dual. Wenninger settled for both segments, forming an unbroken line, and faces similarly duplicated, forming prisms between the edges. It is significant in the present context that neither segment actually crosses infinity but merely terminates there. Thus, he respected the choice of the segments which do not cross infinity. However, by including both segments as edges, he abandoned the primary aim of consructing the dual graph.
However in projective geometry the two directions do meet again, so to prevent the structure from encircling space as a toroid we are forced to choose one arbitrary direction. This breaks the symmetry. Thus we can see what a profound effect the particular space we are working in may have on our treatment of polyhedra and their duals.
Vertex figures
Within the abstract structure of a polyhedron, we may find embedded the structures of various abstract polygons. In its Hasse diagram, we find embedded the diagrams of these polygons. I will call such embedded polytopes sub-polytopes, or just subtopes, of the polyhedron. We may now distinguish, for example, between a face element or piece of the polyhedron and the associated face subtope. Geometrically, the face element is the open polygon, i.e. excluding its boundary, while the face subtope includes the various pieces of the boundary. In what follows, "face" unqualified refers to the subtope.
When a polyhedron is dualised, each face is transformed into a vertex figure of the dual, and vice versa. There is thus a duality between faces and vertex figures. This duality is exemplified by the Dorman Luke construction, noted earlier for the duals of the uniform polyhedra.
The principle applies for all polytopes. Every cell is dual to a vertex figure of the dual polytope.
When we dualise a polyhedron by reversing its ranking direction, we also reverse the ranking direction of the subtopes buried within it. When a face is dualised in this way, the dual polygon is realised as the set of pieces incident on a given vertex, known as a vertex star. But if we ignore the main figure and just number the ranks of the subset in its own right, then we may concretize it as a true polygon, the vertex figure. We can think of it geometrically as a slice through the vertex star.
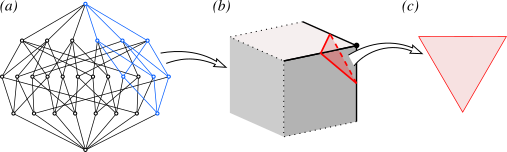
(a) Abstract vertex (blue), (b) vertex star (black), (c) vertex figure (red) of the cube.
Abstractly, this dual vertext figure is still the original abstract face, just with its ranking order redirected and renumbered.
Geometrically, the dual relationship still holds for projective polarisation. The intersection of the original face plane with the polarising sphere is a circle (which may be imaginary). Reciprocating the face in this circle yields a dual vertex figure. The difficulties over crossing infinity and choice of segments and angles do not go away.
Conclusion
So, can we reach any final theory? How have our four appropaches to polyhedral duality fared in this analysis?
Euclidean convexity is confirmed in its limited applicability, as a tool of value only in the simplest of cases. Nevertheless, those cases are of great importance elsewhere and the approach should not be denigrated on its own account; just, it must be used with caution and not let out of its comfort zone.
The breaking of reciprocity might leave us with the impression that, in constructing a dual to some polyhedron, we are in essence seeking to construct the dual graph on the same (i.e. an isomorphic) topological manifold. We use projective reciprocity merely as a tool to help define a concrete geometry for the dual. But we have to recognise that, as a tool used for this purpose, even in projective spaces reciprocity has its limits.
However the abstract inclusion of anaploid pieces breaks even the methods of topological analysis and graph theory. Again, these are reduced to mere fallible tools to our end when we must consider a piece's interior topology in order to define the manifold, and to construct the piece's dual vertex figure on it. Topology as a descriptive discipline does stand up here, as it is needed to describe the interior. But its standard methods do not apply directly to the abstract form.
Last man standing is abstract theory, the description of a polytope as a certain kind of partially-ordered set. Turning the Hasse diagram upside down is so simple, elegant and robust a procedure that it can never be bettered. Key to abstract theory's role in dualising polyhedra has been the two-step process of realization; first the interpretation of the poset as a morphic polytope (employing that same consideration of interior topologies), and second its concretization as a geometric one. Just how well that second step fares will depend both on the kind of space it is being embedded in, and on the chosen method of embedding, such as projective polar reciprocation.
To round things off, the issue as to whether "every polyhedron has a dual" can now be answered. Yes, we can say that abstractly every polyhedron has a dual, and that morphically every polyhedron drawn on a manifold has a dual polyhedron on the same manifold. But geometrically, there is no universal answer; some sort of dual can always be constructed, but whethere you find it acceptable depends on how you define your polyhedra, what you regard as a valid dual, and whether or not you seek a one-to-one correspondence between particular concrete examples. Or, to put it another way, every polyhedron has a dual, but it might not be the one you wanted.
References
- Cundy, H.M. & Rollett, A.P.; Mathematical Models, 2nd Edn, OUP (1961).
- Edwards; Projective Geometry, 2nd Edn, Floris (2003).
- Gailiunas, P. & Sharp, ; "Duality of Polyhedra", Internat. Iourn. of Math. Ed. in Science and Technology, Vol. 36, No. 6 (2005), pp. 617-642.
- Grünbaum, B.; "Graphs of Polyhedra; Polyhedra as Graphs", Discrete Mathematics,, 307 (3–5) (2007), pp. 445–463.
- Grünbaum, B. & Shephard, G.; "Duality of Polyhedra", In Senechal and Fleck (Eds), Shaping Space – A Polyhedral Approach, Birkhäuser (1988), pp. 205-211. Reprinted as Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination, Springer (2013), pp. 211–216.
- Lakatos, Imre; Proofs and Refutations, CUP (1976).
- Wenninger, M; Dual Models, CUP (1983).