^Top

Polytopes, Duality and Precursors

Updated 6 May 2022

My idea of polytope precursors had its roots many years ago in the duality of stellation and facetting. It has evolved over time and this study has been substantially rewritten and renamed – twice. What I now call precursors were first called 'generators' and then 'templates', but for technical reasons those terms proved unsuitable. The developing mathematical foundation turned out to be more or less inherent in modern abstract theory and, in recasting it in abstract terms, I discovered flaws in both approaches. More recently the idea has arisen in theoretical physics of a 'schema' with an underlying 'common core' and it seems a useful concept to adopt here, despite the possible potential for confusion with the "polyschema" of others. In the context of polytopes, I call this common core a precursor.

Contents

Introduction

Despite over two millennia of academic study, mathematicians have struggled to come up with a satisfactory formal definition of polyhedra and higher polytopes. In 1994 Grünbaum referred to this failure as "The original sin in the theory of polyhedra".[1] Nowadays we have come to understand a polytope to be a geometrical "realization", an injection into some containing space, of a particular kind of set-theoretic structure known as an abstract polytope. The abstract construction actually tells us very little about the form of some real geometrical object. Without a rigorous definition of the realization process, we may have little idea what geometrical properties the resulting polytope might have, so this is not much of an advance. However it can shed useful light on the duality of polyhedra.

The duality of polyhedra and polytopes, and their mutual construction via a polar reciprocity, is well known. Abstract theory dualises a polyhedron extremely elegantly, simply by reading its structural Hasse diagram upside down. Projective geometry and the abstract formulation thus present elegant models as far as they go, though each is limited in its own way. Fortunately these limitations need not concern us here.

This essay explores an alternative model for geometric polyhedra and polytopes, based on the need to define the structure and geometry of vertices as well as faces. Development of this idea leads to a less limited model of polyhedral duality, via a level of order underlying all dualities. In the context of polytopes I refer here to this level as precursors.

But before getting started, I should note some more terms and ideas I will be adopting; others may be introduced later on, where appropriate.

A mathematical space can have many dimensions, in general p. A polytope, or p-tope, is a certain kind of closed geometric figure in p-space. A polytope in zero dimensions is a point or vertex, in one dimension a line segment or ditelon, in two a polygon, three a polyhedron, four a polychoron, and so on. The bounding "surface" of any polytope (higher than the 0-polytope) may be built up by assembling polytopes of one dimension lower, here called cells; a cell of a polygon is a side, that of a polyhedron is a face, and so on. The examples in this essay seldom venture beyond three dimensions, and it is not necessary to understand those that do in order to follow the main argument.

It is normal to speak universally of vertices and edges. It will sometimes be convenient here to distinguish between the vertices and edges of a polyhedron or higher polytope, the corners and sides of a polygon, and the ends of a line segment.

The topological structure of a polytope is distinguished from its geometrical form. Many problems with earlier definitions arose from the failure to distinguish topological properties from geometrical ones. For example, faces would typically be defined in the same sentence as having both topological properties such as connectedness and geometric properties such as flatness, making it difficult to see which properties might be the more fundamental, or which might be adapted to other situations, such as say bubbles or foams, without damaging the underlying theory. We say that a geometrical polytope is some realization of the corresponding topological polytope. Likewise, the topological object is some abstraction of the geometric one. Indeed, an abstract polytope represents the highest level of abstraction.

The importance of vertex figures

A polytope is sometimes said to be a collection of its surface features, such as points, lines, planes and so on. One problem with this simple view is that the spatial relationships of the various features are not necessarily determined. For example some collections of features can be assembled in different orderings, or topologies, to create different shapes, as with the rhombicuboctahedron and Johnson solid J37 (the elongated square gyrobicupola). Some can be assembled in different geometric arrangements having the same topology, as with the convex and great regular dodecahedra, or with the regular icosahedron and the irregular one formed by inverting a "pyramid" of five adjacent faces. In order to distinguish between such isomers we need information about both the relative orientations of the faces, and the way in which faces and edges are connected. For example the two icosahedra mentioned differ only in the orientation of their faces, while the regular and great dodecahedra differ only in the order in which their faces are connected. All that assumes that say all edges are the same length, which is not usually the case. For example a figure which is structurally a cube may turn out in fact to be a cuboid, a parallelepiped or something even less regular.

One way to provide the missing information is via coordinates, i.e. applying a metric to the containing space such as the customary Euclidean space. However any polyhedron thus defined has a specific scale and orientation in space, which makes comparisons between different polyhedra tiresome and consequently makes generalisation unnecessarily cumbersome. Another way is via angles, as in conformal geometries. But here, once we move into three or more dimensions, solid angles do not have an exact geometry. For example if we assemble four polygons around a vertex, we can obtain a given solid angle in either of two ways, by pushing one or other pair of opposing edges together an appropriate distance, even though each polygon remains rigid. The dihedral angles between faces at each edge will give us the information we need, provided we know which faces are connected along which edge.

Vertex figures offer a more elegant way to provide all this information. A vertex figure of a polyhedron may loosely be thought of as the polygonal surface revealed when a corner of the polyhedron (in the everyday sense of a corner) is sliced off; many specific definitions are discussed in my essay on vertex figures. The kind of interest here will be defined later. The structural connectivity of faces and edges around the vertex is shown by the connectivity of the sides and corners (in the polygonal sense) of the vertex figure. The dihedral angles between faces can be deduced when required, from the corner angles of the vertex figure and its geometrical relationship with the associated vertex.

The idea of vertex figures generalises to other dimensionalities. In four dimensions the cut surface is a polyhedron, and generally in p dimensions it is some (p-1)-tope. In two dimensions it is just a line or ditelon, which I will sometimes call the corner figure. Different corner figures are characterised by their various lengths. In one dimension the vertex figure is just a point, which I will sometimes call the end figure.

When a polytope is constructed, the geometry of each cell alone is not enough to define the final figure. For example there is nothing to stop one or two caps of five triangles on a regular icosahedron from being inverted into dimples. There are even breathing polyhedra which can smoothly accommodate a range of angles just as a quadrilateral can. In order to fully define the geometry of the whole figure, the geometries of the vertex figures are also needed.

Conversely, the local geometry at each vertex is insufficient. For example they are identical for every cuboid, so these polyhedra cannot be distinguished. It is therefore necessary to include the geometries of the faces.

Thus, to fully define the geometry of a given polyhedron, it is necessary to define that of each cell and vertex figure. Only in this way the coordinates of each part of the figure can be uniquely determined and the geometry of the polytope thus fully defined.

Coxeter finds it convenient to define a regular polytope as one having regular faces and regular vertex figures.[2] It is a short step to observe that, more generally, any polytope in general would similarly be defined by its cells and vertex figures. Coxeter chose this definition for its simplicity. It is the great beauty of mathematics that simplicity and power often go together.

We now modify our hierarchical definition of a polytope accordingly. A 3D polyhedron is now made up of 2D faces and vertex figures. These comprise 1D sides and corner figures, and these in turn 0D vertices and end figures. The hierarchy may be extended upwards to p dimensions.

Abstract polytopes

An abstract polytope captures only the structural connectedness of a polytope, in terms of its elements such as faces and edges, and of their connectedness or incidences. The theory is relatively recent; it is still developing and its jargon evolving, see for example A Critique of Abstract Polytopes. I will try to keep things here as simple and understandable as I can. In particular, abstract theory traditionally generalises the term "face" to any number of dimensions; this can be confusing, especially in the context of polyhedra, so I use the term "piece" for the abstract sense.

An abstract polytope is a set of elements or pieces which are partially ordered by a ranking function and a pairwise relation, referred to as "incidence", between elements of adjacent rank. A polytope of dimension p has ranks j for −1 ≤ j ≤ p, with elements of rank j which I call j-pieces. Thus it has two more ranks than its dimension. There is just one piece each of ranks p and −1, respectively named the maximal and minimal (or null) pieces.[3] The standard diagram depicting the ranked incidence structure is known as a Hasse diagram.

Fig. 1: Hasse diagram of the abstract cube.

The set-theoretic definition imposes certain structural properties which Johnson has summarised as monal, dyadic and properly connected; these essentially bar monsters such as compounds, configurations, elements being repeated, and so on.[4] One important property which is allowed, is the presence of polytope structures with fewer ranks, within the overall structure. I refer to these as sub-polytopes, or "subtopes".

An abstract piece is not a polytope (subtope) in its own right. Rather, it corresponds to the interior or body of such a polytope; for example a 2-piece corresponds to the plane region bounded by the edges of a polygon.

A key distinction is therefore made between a single element or piece and the wider subset which also includes the pieces of lower dimension which form its boundary. These bounding pieces, together with the bounded piece and the connected piece of one rank lower than the lowest-ranked boundary pieces, do form a polytope in its own right. For example a polygonal face subtope comprises not only a 2-piece but also the 1-pieces incident with it, the 0-pieces incident with those and the −1 piece which is incident with them in turn. This gives it the correct ranked structure to comprise a 2-polytope. The null piece has no subsidiary pieces and is often treated as its own subtope, the null polytope or nullon. These various polytopes within the overall structure are its subtopes.

Realization and morphic theory

The above abstract formulation says nothing about the geometric appearance of the polytope. A geometric figure must be derived from the abstract formulation through some process of "realization", in which it is mapped or injected into some containing space such as Euclidean space. Standard abstract theory is somewhat woolly about this process, typically only making assumptions about the outcome.

In order to bring some rigour and clarity to issues such as this, I developed morphic theory. This recognizes two distinct steps or stages to the realization process:

Interpretation. This first step defines the objects that each rank of abstract elements represents. They could be tables, chairs and beer mugs for all that abstract theory has to say about them. But we choose such geometrical entities as points (vertices), line segments (edges), surface regions (faces) and so on. The maximal element is the body or interior of the figure and the minimal element is left as a kind of null polytope or nullitope. The incidence relation is defined as a structural, and hence also physical, adjacency or connectivity.

The assemblage of all these elements now comprises a topological manifold, a "rubber-sheet" figure. Morphic theory treats it as a bounded manifold, the boundary being the polyhedral surface and the rest of the manifold its body. This contrasts with the more traditional twentieth-century focus on the bounding surface, harking back specifically to the original idea of a solid body.

Concretization. The second step is to inject the manifold into some geometric space, typically one with a metric so that we may give it lengths and angles. It is at this stage that we decide whether the faces should be flat and edges straight, as a conventional polyhedron, or all lie on the surface of a sphere as a spherical polyhedron, or everything lies in a plane as a perspective drawing and therefore geometrically degenerate, and so on.

Duality of polytopes

With the above conceptual and theoretical background established, we can now begin to approach the core thesis of this essay.

Projective duality and reciprocity

The dualities between points, lines, planes and so on are a theorem buried deep within the foundations of projective geometry. One manifestation is the well-known reciprocity of two dual polyhedra about a concentric sphere.

In general, for a polytope of dimension p (where p > 0, since the (−1)-sphere is undefined), reciprocation about some (p−1)-sphere twins it with a dual polytope.

Abstract duality

The dual of an abstract polytope is obtained in a remarkably simple and beautiful way, by reversing the order of ranking. That is all. Ranks p and −1 exchange places, as do ranks p−1 and 0, and so on. The incidence relations remain unaffected.

Thus, the same abstract structure underlies both a polytope and its dual, making it an obvious candidate for a polytope precursor.

Directing the ranking order may be removed from the abstract formalism, instead becoming a part of the first, interpretative stage of realization, along with the appearance of geometric objects such as points and line segments.

The undirected abstract structure, given a ranking sequence but not a direction for that sequence, may be regarded as the highest level of abstraction and therefore also as an appropriate object to form the basis of a true abstract polytope. Ranking order may be imposed for analytical purposes but is not intrinsic to the abstract object, just as homogeneous coordinates perform the same function for projective spaces but are not intrinsic to projective geometry.

Vertex figures and duality

When a polyhedron is dualised, each face is transformed into a vertex figure of the dual, and vice versa. There is thus a duality between faces and vertex figures. This duality is exemplified by the Dorman Luke construction for the duals of the uniform polyhedra (see Figure).

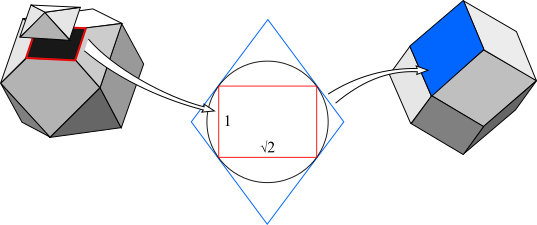
Fig. 2: Dorman Luke construction for the rhombic dodecahedron, showing the duality of face (blue)
and vertex figure (red).

The principle applies for all polytopes. Every cell is dual to a vertex figure of the dual polytope.

Vertex figures and abstraction

A (p−1)-subtope is a cell. Dualising a cell – by reversing the ranking with respect to the whole polytope – yields a dual subtope which I will call a vertex subtope. Its ranks within the dual polytope have dimensions 0 to p.

When the dual polytope is realized as a whole, the vertex subtope is realized as the set of pieces which are incident on the given vertex, up to and including the body. Such a construction is called a vertex star.

A vertex subtope has the same number of ranks as a cell, but it is shifted up one rank overall, from −1 ≤ j ≤ (p−1 to 0 ≤ j ≤ p). If it is realized with the same ranking level as a cell subtope, i.e. one level lower than the star, then it is realized as the vertex figure. The vertex figure may now be understood as a lower-dimensional slice through the vertex star.

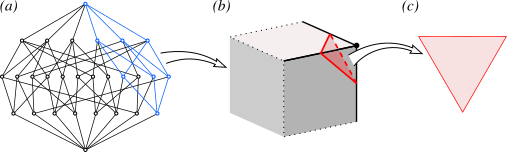
Fig. 3: Vertex subtope (blue), vertex star and vertex figure (red) of the cube.

When a vertex subtope is realized, its appearance thus depends on the chosen mapping; map it to its full dimensionality and it appears as a vertex star, but map it to one dimension lower and it appears as a vertex figure.

Thus, Coxeter's choice of both cells and vertex figures as definitive does not quite match abstract theory. It would be more direct to define a geometric polytope in terms of its cells and vertex stars. However the vertex star carries a great deal of redundant information, for example many if not all of the other elements may be deduced from the shape of the body alone. The vertex figure eliminates all this redundant information.

More useful still to the geometer, if the vertex figure is taken in the same plane as the dual face, then the two figures are themselves duals within the plane, each obtained from the other by reciprocating about the conic where the plane intersects the main reciprocating quadric (usually intersecting a sphere to form a circle.

Since both realizations of the vertex subtope have the same structure, it does not matter at a theoretical level which one works with. For many purposes, the vertex figure is the more convenient.

Polytope schemas and precursors

Schemas in theoretical physics

Symmetries and dualities are not purely geometric phenomena, but also provide some of the most fundamental underpinnings of modern theoretical physics. Duality itself has come to be seen as a kind of "giant symmetry". One such duality is found in the relationship between gauge field theories of physics, exemplified by quantum field theories, and the less conventional unified gravitational string theories in ten or eleven dimensions.

De Haro and Butterfield have recently highlighted the treatment of duality as a symmetry and from that notion have been developing the idea of an overall "schema" in which a common core, a "bare theory", is expressed in two dual physical theories, gauge and gravity respectively, which are mathematical isomorphs or "isomorphic models" of the bare theory.[5]

They note that their schema principle is extremely broad and has much wider scope than the dualities they happen to be interested in.

It is a short step to exploring its relevance to the duality of polytopes, with some kind of common core forming a precursor to two dual polytopes. An abstract polytope, defined as above with an undirected ranking, has both the necessary rigour and the necessary generality to form the basis for a bare theory of polytopes, providing a common core model or precursor for a dual pair of morphic or geometric polytopes.

The sequence of ranking may be interpreted in either of two directions, yielding a dual pair of polytopes. The underlying precursor, together with the ordering process and the resulting duals, comprise the schema for the polytope.

Abstract precursors

The cell and vertex subtopes are examples of the more general span and cospan of a piece. The spans of one polytope are dual to the cospans of the dual polytope. For some piece F of P, the subtope F/F−1 is also referred to as the span of F, and the subtope Fp/F as the cospan of F. The span of a (p−1)-piece is a cell subtope. The cospan of a vertex is a vertex subtope. The subtope F/F is just F. The span of Fp is P and its cospan is Fp, while dually the span of F−1 is F−1 and its cospan is P. The span of an edge is the edge subtope comprising the edge piece itself, two monons and the nullon. Its cospan is what one might call an edge star, comprising the edge piece, two face pieces and (in a polyhedron) the body.

The cell spans and vertex cospans of an abstract polytope are, collectively, its (p−1)-dimensional subtopes. The set of p−1 dimensional subtopes of an abstract polytope thus comprises two subsets, its cell subtopes and its vertex subtopes. Which subset is which depends only on the dimension and ordering of their ranks. This set of spans and cospans may be shorn of any absolute dimensionality in the same way that the abstract polytope was to create the undirected precursor.

More generally, all the spans and cospans having a given number of ranks may be treated in the same way. In its undirected form, each abstract subtope represents a precursor both to the span of some piece of a polytope and to the cospan of the dual piece of the dual polytope.

Construction of geometric polytopes

It now becomes natural to define a given geometric polytope as a realization of its precursor. The precursor must follow the two-step realization process, first being interpreted as one of two dual morphic polytopes and then being concretized with a specific geometry.

The detailed geometry may be constructed, after Coxeter, by defining the specific geometry of each face and vertex figure. This need only be done ab initio for one of the pair; the relevant geometries of the dual may typically be derived from the original via polar reciprocity about the quadric surface (typically a concentric sphere) which defines the particular dual relationship.

Symmetrical precursors

If every piece of an abstract polytope is uniquely labelled, then the various subtopes can be labelled accordingly. But there are usually large quantities of both pieces and subtopes, which makes for tedious enumeration. Life is simpler for highly symmetrical polytopes. Here, there will be several groups of congruent pieces, each group lying in its own symmetry orbit. This will create equivalent subtope groups and orbits.

In order to describe some geometric polytope, it is then only necessary to describe one face and one vertex figure from each group. Moreover, in each such figure it is only necessary to identify the group in each orbit of congruent pieces, rather than every specific piece.

In a dual pair, the symmetry groups remain unchanged, while their orbits may differ. Assuming that symmetry is to be preserved, then reciprocation about a concentric sphere is necessary. The orbits then differ from their duals only in scale. This constancy of groups allows the same labelling to be used for both polytopes.

In this way, a single labelled subtope can act as the generator of a labelled face subtope of one polytope and a labelled vertex figure of its dual. Fig. 4 shows an example labelling of the construction from Fig. 2. In the vertex figure, E is the group containing the single null polytope, as is A in the face.

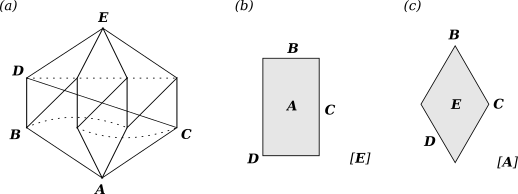
Fig. 4: Precursor (a) of the vertex figure (b) and face (c) from Fig. 2.
The symmetry groups are labelled in bold.

This result finally achieves my purpose in developing the theories of morphic polytopes and precursors, and it is my intention next to apply it to stellation and facetting, especially with respect to the regular icosahedron and dodecahedron. I have made a start on the icosahedral precursors.

References