Tidy Dodecahedra and Icosahedra

More findings on stellation and facetting

by
Guy Inchbald

Updated 2 Mar 2024

Abstract

Bridge's 1974 paper is revisited. Tidy facets of the regular dodecahedron are listed. Tidy facettings, and their reciprocal stellations of the icosahedron, are enumerated, including a rediscovered lost stellation and some infinite ones. The stellations are compared with the fully suppported stellations. Du Val's notation for the stellated icosahedra is extended.

Change history

2 Mar 2024. Minor clarifications on tidiness.
28 Nov 2023. General cleanup and minor update.
29 July 2004. Updated following correspondence with N J Bridge. "Faceting" now "facetting". Other minor edits.
25 June 2004. Added notes on Bridge (1974) and some other significant updates. Subtle name change.
11 Dec 2003. Added references to Wenninger's Dual Models, and other minor details.
20 April 2003. First stable version.

Introduction

This is the third in a series of papers attempting to revisit the stellations of the regular icosahedron and their duals, the facettings of the regular dodecahedron. The ways of journal publishers led to the second paper [1] being dated some two years earlier than the first [2]. Unlike its predecessors, this one has not been published elsewhere.

After "finishing" the present paper, Bridge's [3] came to my attention and I realised that most of this paper, together with parts of my second, were substantially a rediscovery of his findings, though using a different notation and sometimes with different interpretation of the results. Some of these new interpretations are important, especially in the light of general changes in attitude over the intervening years. I therefore revised this essay fairly extensively to discuss Bridge's results, both to take them further and to rescue them from an undeserved obscurity.

Before continuing, I should explain some of the terms which Bridge and I employ. References to the icosahedron and dodecahedron are of course to the regular varieties.

A facet is a face sharing certain vertices of a convex polyhedron, and is located entirely within its interior. The process of exposing such facets to create a new polyhedron is "facetting" or "faceting", spelled according to taste. The resulting polyhedron is a "facetting" or "facetion"; Bridge uses the latter term due to its resemblance to "stellation", however the former is more grammatical. Facettings of the dodecahedron are sometimes referred to as facetted dodecahedra or just dodecahedra. While this is technically incorrect since most of them do not have twelve faces, they do all share icosidodecahedral symmetry.

A polyhedron may have a complex internal structure. The visible outer surface, having no internal structure, forms a polyhedron which is its surhedron. This is distinct from its convex hull, which is just the original polyhedron.

A compound polyhedron is a set of polyhedra sharing a common centre and disposed symmetrically - here with icosidodecahedral symmetry. We recognise as atomic stellations or facettings just those compounds where the polyhedra are congruent. Those with non-congruent polyhedra are treated as non-atomic compound stellations or facettings of lesser interest.

It will sometimes be convenient to distinguish between the edges of a polyhedron on the one hand, and the sides of a polygon on the other.

A topological dual of a polygon or polyhedron is a more general idea than its geometric reciprocal, which is the dual figure obtained when the polygon or polyhedron is reciprocated with respect to some conic or quadric, by convention a concentric circle or sphere. Whilst the reciprocal of a polyhedron can always be obtained, it may not always be an acceptable polyhedron. Where it is not acceptable we may still speak of "the dual" (as for example with Wenninger's infinite hemi-duals).

Much has been written on the phenomenon of overlapping figures. For example, is the regular hexagon { 6/2 } a pair of concentric triangles with their vertices alternating around a convex hexagon, or is it a double-wound triangle, with two vertices at each geometrical apex? Or, is a digon a respectable polygon? It can be drawn on a sphere and polyhedra comprising multiple digons, known as hosohedra, constructed, but when it is flattened down with straight sides, they superimpose and it has zero area. In this essay I introduce the idea of "tidiness" to describe a figure from which such phenomena are absent. Of course, which phenomena should one regard as untidy and why? In practice, opinions have often been unconscious or based on the needs of the moment, and tend to differ. Tidiness is a subjective judgement on, not an objective property of, a polyhedron.

Tidy facets

I will take the view here that a tidy polygon is one which is finite and admits an unambiguous circuit, having no coincident edges or coincident vertices. Bridge is somewhat stricter, requiring also that no polygon may have edges which are collinear (his rule 5) or pass through the centre (rule 8). Rule 5 primarily affects stellations, where collinear edges may reciprocate to coincident ones. Rule 8 is most relevant to facetting, where facets and edges passing through the centre reciprocate to vertices and edges located at infinity.

These two rules are designed to ensure that the reciprocal figure is also acceptable; Bridge took the view that, for a stellation or facetting to be acceptable, its dual must be so as well. While I agree with this principle, I am not prepared to dismiss a tidy figure simply because its reciprocal is untidy. Rather, I extend the criteria for acceptance to embrace the figures encountered. For now, we may note generally that a tidy figure need not have a tidy reciprocal, and specifically that hemi facets (called "diagonal" by Bridge) are acceptable.

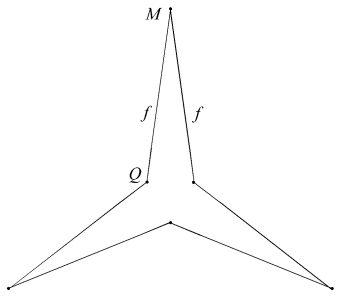
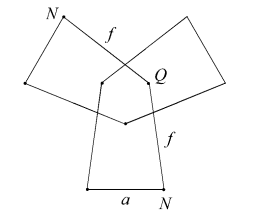
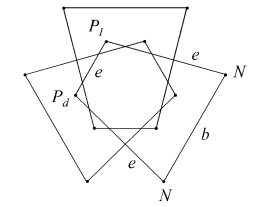
The facet planes of the dodecahedron lie in sets or symmetry orbits which, working from the outside in, may be identified as A to K. Similarly, the possible edge sets are m to s. These are illustrated in [1].

For certain facet planes, different sets of edges can be chosen to give different facets. For example in A, we may choose either edges m to form the sides of a convex pentagon, or edges n to form the sides of a pentagram. These may be represented as Am and An respectively. Where edges are chiral, as in p, they may be divided into dextro (right handed) and laevo (left handed) sets, as p_d and p_l.

The tidy facets are listed in Table 1, together with certain properties of their sides. The first row gives the total edges in each group. Sides which form closed edge groups are denoted by boxes. If all the sides of a facet do so, then the facet set forms a closed polyhedral surface in its own right. Note that Bridge does not give sufficient information to orient his two variants of {2,2bc}, so I have assigned them arbitrarilty to the two variants of Cnp.

Facet		Sides						Comments
As text	Bridge	m	n	pl	pd	q	s
		30	60	30	30	30	10	Number of edges in group.
Am	{0,5a}	60	-	-	-	-	-	Closed.
An	{0,5b}	-	60	-	-	-	-	n open.
Bn	{1,3b}	-	60	-	-	-	-	n open.
Cnpp	{2,2(bc)}	-	60	30	30	-	-	n, pl and pd open.
Cnrp	{2,2(b'c)}	-	60	30	30	-	-	n, pl and pd open.
Cn	{2,4b}	-	120	-	-	-	-	Closed.
Dmp	{3,acc}	60	-	60	60	-	-	Closed.
Enp	{4,bcc}	-	60	60	60	-	-	n open.
Fmn	{4,3(ab)}	60	60	-	-	-	-	n open.
Fmq	{4,3(ad)}	60	-	-	-	60	-	Closed.
Fnq	{4,3(bd)}	-	60	-	-	60	-	n open.
Fpl	{4,3c}	-	-	60	-	-	-	Closed. Chiral.
Fpd	{4,3c}	-	-	-	60	-	-	Closed. Chiral.
Fp	{4,6c}	-	-	60	60	-	-	Closed. Comp'd of Fpl and Fpd.
Gn	{5,5b}	-	60	-	-	-	-	n open.
Gq	{5,5d}	-	-	-	-	60	-	Closed.
Hpq	{7,ccd}	-	-	60	60	60	-	Closed.
Jmq	-	30	-	-	-	30	-	No pair available for q.
Jms	-	30	-	-	-	-	30	s is untidy (trimethoric).
Jqs	-	-	-	-	-	30	30	s is untidy (trimethoric).
Knp	-	-	60	30	30	-	-	n, pl and pd open.
Kns	-	-	60	-	-	-	60	s is untidy (hexamethoric).
Kps	-	-	-	30	30	-	60	s is untidy (hexamethoric).

Tidy facettings

The term "polyhedron" has been applied to a wide variety of three-dimensional forms. A tidy polyhedron is one which conforms to the more standard definitions [1]. We can say that it comprises a finite, irreducible closed set of finite-sized flat faces which bound a region of space, and any edge joins exactly two vertices and two faces. Its faces and vertex figures are tidy polygons.

In Table 1, sides which count only once per edge are joined to only one facet and so are open and available for joining to facets in other groups, those which count exactly twice are joined to two facets and so are closed edges within their group, and those which count more than twice form untidy edges.

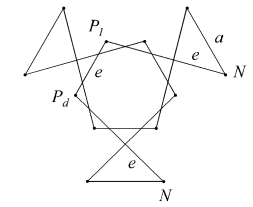
Nine facet sets close to form tidy polyhedra, or eight if we count any enantiomorphic pair as a single solution (which we will generally do from now on. For stellations it is customary to describe the dextro forms only, so for facettings it is convenient to describe their reciprocals which are the laevo forms). These include the dodecahedron itself and seven facettings.

Every occurrence of s has more than two faces meeting at an edge, and so can not form a tidy polyhedron. There is only one remaining open set of q, which therefore has no opportunity to join with another face. These two observations rule out every hemi face except for Knp, which joins with either Cn_p or Cn_r (the _p and _r subscripts will be explained later).

Six face sets remain, all open at n. Any must join with exactly one other to close n. There are 15 possible combinations, of which the coplanar pair FmnFnq is not tidy, leaving 14 tidy facettings.

This yields a count of 7 + 14 = 21 facettings, plus the original dodecahedron, making up the 22 derived in this manner by Bridge. There are also the 2 hemi facettings he rejected, making 24 in all. These are listed in Table 2, together with the reciprocal stellations of the icosahedron.

Labelling of the vertex figures and face circuits in the table derives from the stellation and facetting diagrams in [1]. Use of the same letter for reciprocal features allows the respective circuits around a face and its dual vertex figure to have the same letter sequence, with the exception that the dextro and laevo edges, p_d and p_l, are reciprocal. Capitals indicate points and lower-case letters indicate lines. A circuit around a vertex figure starts at a side (lower case), whereas that around a face starts at a vertex (capital). The capitalisation thus indicates which figure is identified. Where the letter sequence repeats, the repetitions are omitted for brevity. Multiple non-congruent circuits in a figure are separated by tildes ( ~ ). This notation provides a useful tool in tracing out reciprocal figures on the stellation and facetting diagrams.

The Du Val symbols are taken from [4]. They are not related to the other notations.

Facetting				Reciprocal stellation
Comments	Faces		Vertex figure	Du Val symbol	Face circuit
	As text	Bridge
Regular facettings
{5, 3}	Am	[0,5a]	aM	A	Am
{5/2, 3}	Gq	[5,5d]	gQ	G	Gq
Comp of 5 cubes	Cn	[2,4b]	cN	C	Cn
Comp of 5 tet	Fpl	[4,3c]	fPl	Ef1	Fpd
Comp of 10 tet	Fp	[4,6c]	fPl~fPd	Ef1	Fpd~Fpl
Uniform facettings
3 | 3 5/2	AnBn	[0,5b; 1,3b]	aNbN	B	AnBn
3 | 5/3 5	AnGn	[0,5b; 5,5b]	aNgN	De2f2	AnGn
3/2 | 3 5	BnGn	[1,3b; 5,5b]	bNgN	De2f2	BnGn
Other facettings
	Dmp	[3,acc]	dMdPddPl	D	DmDplDpd
Self-dual. Hollow.	Fmq	[4,3(ad)]	fMfQ	Ef1g1	FmFq
	Hpq	[7,ccd]	hPdhPlhQ	H	HplHpdHq
	AnEnp	[0,5b; 4,bcc]	aNePdePleN	De2	AnEplEpdEn
	AnFmn	[0,5b; 4,3(ab)]	aNfMfN	De1	AnFmFn
	AnFnq	[0,5b; 4,3(bd)]	aNfQfN	Ef1g1	AnFqFn
Comp of 10 tri antip	BnEnp	[1,3b; 4,bcc]	bNePlePdeN	De2	BnEpdEplEn
	BnFmn	[1,3b; 4,3(ab)]	bNfMfN	De1	BnFmFn
	BnFnq	[1,3b; 4,3(bd)]	bNfQfN	Ef1g1	BnFqFn
	EnpFmn	[4,bcc; 4,3(ab)]	ePlePdeNfMfN	E	EpdEplEnFmFn
	EnpFnq	[4,bcc; 4,3(bd)]	ePlePdeNfQfN	Ef1g1	EpdEplEnFqFn
	EnpGn	[4,bcc; 5,5b]	ePlePdeNgN	Df2	EpdEplEnGn
	FmnGn	[4,3(ab); 5,5b]	fMfNgN	Ef2	FmFnGn
	FnqGn	[4,3(bd); 5,5b]	fQfNgN	Fg1	FqFnGn
Hemi facettings
	CnppKnp	-	cPlkN~kPdcN	Hj2	CpdKn~KplCn
	CnrpKnp	-	cPdkN~kPlcN	Hj2	CplKn~KpdCn

Edge facettings

An edge facetting has the same edges as the original polyhedron, as well as the same vertices. An example is offered by the great dodecahedron, which is an edge facetting of the icosahedron. The regular dodecahedron has no edge facettings, other than the trivial example of itself, Am.

Regular and uniform facettings

Faces Am, An, Cn, Fp_l, Fp_d, Gn and Gq are all regular. Because a facetting has congruent vertices, those constructed from only these faces are uniform. There are eight such facettings, including two regular polyhedra and three regular compounds (counting the two chiral compounds of five tetrahedra as a single solution). They are listed first in Table 2. All are well known and are illustrated for example in [5] as well as [3]. Their seven outwardly distinct reciprocal solids are likewise well known and are illustrated in [4].

The two occurrences of De₂f₂, noted in [1], can now be distinguished as respectively having faces AnGn and BnGn. They are two quite distinct polyhedra, differing as they do in their internal structure, density and topological genus (The density of a polyhedron may be found by counting the number of times the central region is "wrapped" by the surface, and the genus via a modification of Euler's formula as ¹/₂(2−V+E−F). Bridge tabulates their values for all of his polyhedra). Analyses of stellations according to cell aggregates or surhedra are unable to distinguish between these polyhedra, and therefore to explain the existence of two uniform facettings reciprocal to a supposedly single stellation.

Other tidy facettings

The remaining 14 facettings described by Bridge are also geometrically tidy, and are illustrated below. Each is identified by its face sets, or types, followed by a 3D view and vertex figure. The edges are identified in the vertex figures.

Dmp
Fmq
Hpq
AnEnp
AnFmn
AnFnq
BnEnp
BnFmn
BnFnq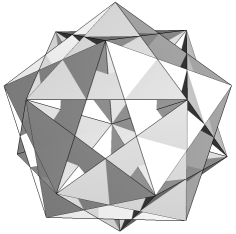
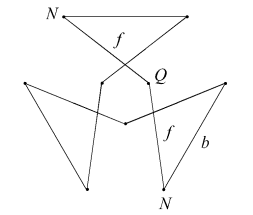EnpFmn
EnpFnq
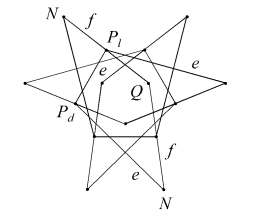EnpGn
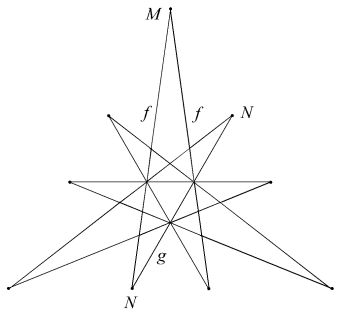
FmnGn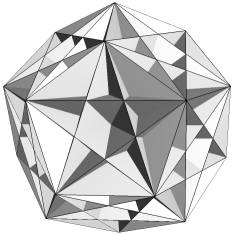
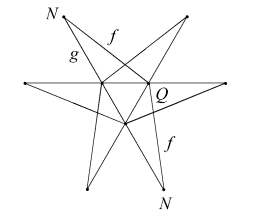
FnqGn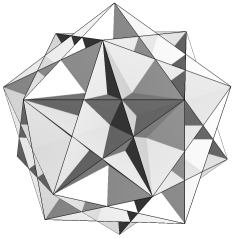

Some of the vertex figures have multiple sides coincident at certain vertices, suggesting at first sight that they are untidy. However, in each case only two sides end at the vertex - the other edges pass through it and for them it is a "false" vertex. There are thus no superimposed vertices, so one might wish to regard them as tidy.

Three of these other facettings have only a single face type. Fmq is a self-dual form of the well-known deltahedron. Bridge observed that its icosahedral core has density 0, so the polyhedron has an internal cavity. Dmp has slightly shallower dimples (and is not hollow). Hpq is a reciprocal to stellation H, the "final" stellation of the icosahedron.

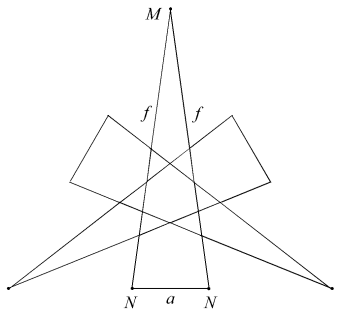
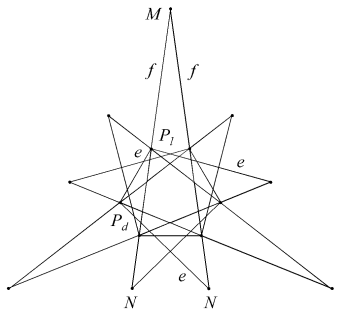
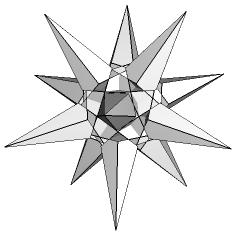
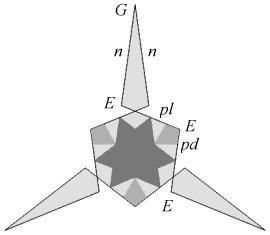
The remainder have two face types. With one exception their duals may be found in the well-known enumeration of 59 [4]. Reciprocal to EnpGn is Df₂ (Figure 1). This stellation is omitted from the 59, being seen as a compound of two separate stellations, D and f₂, so breaking the authors' interpretation of Miller's Rule (v). Bridge refers to it as D+f₂, as if unwilling to accept the consequences of his own discovery. Each face is a tidy dodecagon, derived by reciprocating the vertex figure of EnpGn. The underside edges of the f₂ cells join neatly along the re-entrant edges of D, and the six crossing points at the base of each spike are not true vertices. To treat it as two distinct shells, as previously done, is quite wrong. We have here a remarkably simple and elegant lost stellation, in addition to those mentioned in [1] (which we now understand to be untidy).

Figure 1   Stellation Df2 - 3D view and face EpdEplEnGn

Facetting BnEnp is a compound of ten trigonal antiprisms, and the reciprocal stellation, a form of De₂, is a compound of ten rhombic hexahedra.

Some tidy facettings reciprocate to isosurhedral stellations, i.e. having the same outward appearance. Bridge uses the ideas of density and genus to show that such externally similar forms are in fact distinct stellations. Here, the face circuit makes the same point.

There are nine outwardly distinct stellation forms within this group. Together with the seven outward forms of the eight regular and uniform duals, there are just 22 geometrically tidy stellations of the icosahedron having 16 surhedra. Of the 59 traditional stellations, we now see that only these 16 can be constructed as tidy polyhedra, the remaining 43 are untidy in one way or another.

It is interesting to compare the tidy reciprocal stellation forms with the fully supported stellations, which are those having no underside region of any face visible.

Stellation	Tidy reciprocal	Fully supported	Comments
A			Icosahedron {3, 5}
B
C			Compound of 5 octahedra
D
De1
De2
De2f2
Df2			f2 undercut
E
Ef1			Compound of 5 tetrahedra
Ef1			Compound of 10 tetrahedra
Ef1g1			Deltahedron
Ef1f2	()		Compound stellation of De2f2 and Ef1
Ef2
F	()		Compound stellation of De2f2 and Ef1
Fg1
Fg2			Collinear edges
G			Great icosahedron {3, 5/2}
H			Echidnahedron

Just one fully supported stellation is not a tidy reciprocal; each face of Fg₂ has three pairs of collinear edges, which reciprocate in the facetting to four faces meeting along certain edges. By Bridge's rule 4. this stellation would not even be allowed as a polyhedron. I would say that the stellation is valid and even tidy, while the reciprocal facetting is untidy. Its existence suggest that there may be other tidy stellations whose reciprocal facettings are untidy. Ef₁f₂ and F might appear to exhibit the same characteristic, however they may alternatively be derived as compound stellations comprising the tidy reciprocals De₂f₂ with respectively five or ten tetrahedra.

Just one tidy reciprocal, the rediscovered Df₂, is not fully supported, the undersides of the f₂ cells being visible.

Hemi facettings

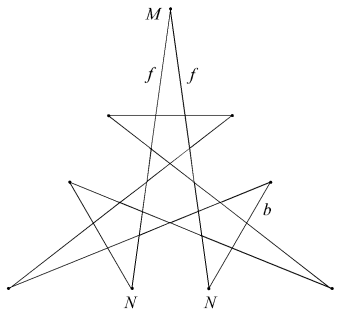
In Euclidean space, if a face plane passes through the centre of the reciprocating sphere then the face reciprocates to a vertex located at infinity, and its boundary to an infinite prism. This observation led Bridge to reject the hemi facets and associated facettings, a step which need not follow at all. When a polyhedron having a centre of symmetry is reciprocated, it is customary to align this centre with that of the reciprocating sphere. For a hemi polyhedron, the reciprocal figure will extend to infinity. But if the cenre of the sphere is offset slightly then the reciprocal becomes a finite and tidy polyhedron, at the expense of losing its symmetry. The topology of the reciprocal remains the same throughout, so the infinite figure has the topoplogy of a tidy polyhedron. There is no reason to reject the original figure as a proper facetting simply because we choose to place a reciprocating sphere in an untidy Euclidean relationship with it, and such hemi forms are well established in the literature (See [5] for example).

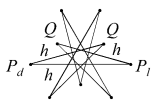
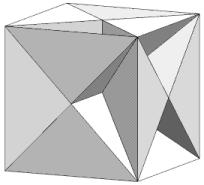
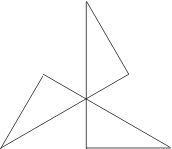
Just two facettings of the dodecahedron are both hemi and tidy. Each is a compound of five hemi facetted cubes. The facetted cubes are unusual in that the vertices are chiral, with alternating dextro and laevo forms around the cube (Figure 2).

Figure 2   Hemi facetted cube - 3D view and vertex figure

In the compounds, dextro and laevo vertices coincide, restoring overall reflective symmetry. The compounds differ in the orientation of the cross-quadrilateral facets. Where the C faces are filled such that they lie in the wider angle between adjacent n edges, giving minimal overlap and a more full appearance to the vertex, the arrangement of edges is said to be prograde, as n_p. Where the C faces are filled such that they lie in the narrower angle between n edges, overlapping more to fill a smaller soild angle and give a more cutaway appearance to the vertex, the choice of edges is said to be retrograde, as n_r.

CnppKnp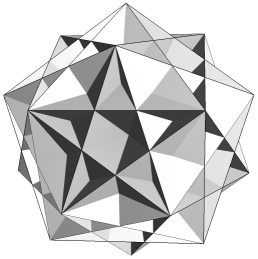
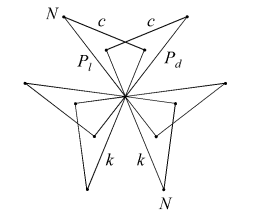CnrpKnp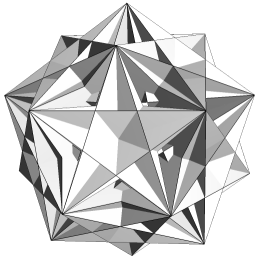

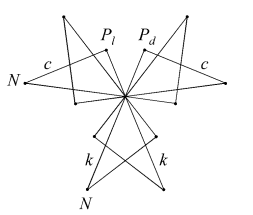Reciprocal to the hemi facetted cube is an infinite octahedron comprising six rhombic prisms. The conventional view is that each prism extends to infinity in just one direction, however it is not possible to retain congruencies or overall geometric symmetry unless each prism has images extending in both directions, as in [1]. This approach may be compared to Wenninger's [6]; he also found that infinite edges can only form satisfactory figures if they extend in both directions. I will not go into the issue here, as to whether these untidy figures should be regarded as polyhedra or as some other kind of figure.

The icosahedra reciprocal to the hemi facettings each comprise thirty such prisms, and can be distinguished apart only by identifying the arrangement of true and false vertices. The intersecting face planes divide each infinite prism into cells, lying in congruent sets. The finite cells are described in [4], but one new type is infinitely long.

Extending Du Val's notation

For those familiar with Du Val's notation for cell aggregates, it is perhaps worth extending it to include such infinite cells. The outermost finite cells are set h. Connected to their outer faces is a layer of infinite cells, which may be identified as j (omitting the letter i from the series). These all have four parallel edges meeting at infinity, and apart from a short region near h, are prismatic. They fall into two subsets: 30 of type j₁ located directly above g₁ and having vertices at infinity which I label J, and 60 of type j₂ above g₂ and having vertices K at infinity. Cells j₁ are not a part of any stellation described here, while cells j₂ combine with all the finite cells, as Hj₂, to form the infinite stellations described.

There are two further infinite layers. k comprises two types of "wedge" having two parallel faces and two diverging faces. The parallel faces meet along edges s located at infinity. k₁ is asymmetric and bridges between types j₁ and j₂. k₂ has reflective symmetry and bridges between two neighbouring j₂ cells. The outermost layer l comprises three types of fully diverging cell, each forming the sides of an infinitely tall pyramid. l₁ is a hexagonal pyramid above e₁ and between six k₁. l₂ is a regular pentagonal pyramid above f₂ and between five k₂. Finally, l₃ is an isosceles triangular pyramid located above h, and between two k₁ and one k₂.

A large sphere around the icosahedron is illustrated, showing lines of intersection with the face planes. Each region of its surface is a section through an infinite cell.

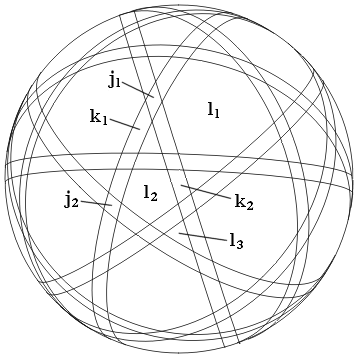
Figure 3   Sphere intersecting the infinite cells of the stellated icosahedron

The dual of any hemi facetting will have cells of the general prismatic type, represented here by j, as noted by Wenninger. The dual of any facetting having edges through its centre will have cells of the general wedge type, represented here by k (such facettings were not studied by Wenninger). Cells of the general pyramid type, represented here by l, are not part of any stellation but rather as parts of "outside" (whatever that may mean) and should at best be regarded as degenerate.

Conclusion

The idea of tidiness is beginning to bring some clarity to the whole mess. While it broadly parallels Bridge's enumeration of the more straightforward facettings and stellations, its subjective nature means that it cannot resolve all the messes it exposes. One result is clear – tidiness is no friend of polar reciprocity! Bridge's discovery of stellations such as De₂f₂ and Df₂ are of particular note.

The fully supported stellations include a number of more basic types, such as the primary, mainline and monoacral stellations [7], so we have also gained some insight into these types; the limitations of the associated analyses in terms of cell aggregates or surhedra are evident.

From here on the faces and vertex figures will become more complicated and difficult to treat with rigour. The permissible facets in A, G and especially F will require careful analysis. A variety of infinite stellations may also be encountered.

Software

The 3D views of polyhedra were produced using the Great Stella program for PC.
Great Stella will also create vertex figures, nets, VRML models, and much else.

References

1. G. Inchbald, "Towards stellating the icosahedron and facetting the dodecahedron", Symmetry: Culture and Science Vol. 11, 1-4 (2000) pp. 269-291.
2. G. Inchbald, "In search of the lost icosahedra", Math. Gaz. 86 (July 2002) pp. 208-215.
3. N. J. Bridge, "Facetting the dodecahedron", Acta Crystallographica A30 (1974), pp. 548-552. (PDF copy)
4. H. S. M. Coxeter (et al), The fifty-nine icosahedra, 3rd Edition, Tarquin (1999).
5. H.S.M. Coxeter (et al), Uniform Polyhedra, Phil. Trans. 246 A (1954) pp. 401-450.
6. M. Wenninger, Dual Models, CUP (1983).
7. R. Webb, Stella: polyhedron navigator, Symmetry: Culture and Science Vol. 11, 1-4 (2000) pp. 231-268.