Some Lost Stellations of the Icosahedron
Updated 10 May 2022
Change history
10 May 2022. Candidates from my old printouts.
15 Mar 2017. Attribution to Hugel.
11 July 2006. Two lost models rediscovered, attributable to Flather. List re-ordered according to size. Other minor corrections/improvements.
8 Jan 2006. Image of the infinite stellations Hj2 that are dual to the two compounds of five hemi facetted cubes (It's the last example on the page).
Contents
1. Introduction
This page brings together many of the lost stellations of the icosahedron that I have come across so far, along with some representative borderline cases. There are others that I have not had time to include, notably four studied by Grünbaum, as well as several in my computer printouts. None of these stellations conform to Miller's rules, and so do not appear among the eponymous fifty-nine. Nevertheless, all or most of them are properly significant and distinct stellations. I have attributed the discovery of each to the earliest reporter I know of - two go back to H.T. Flather; it is likely that he discovered these around 1930. Where no attribution is made, then as far as I know I am the discoverer.
I have broadly divided the page into "true" and "candidate" lost stellations. As my researches progress, this division is looking less and less sensible. At some point I will have to revise it heavily, or perhaps even abandon it as meaningless.
The following information is provided for each stellation:
Index Number: The Code number as explained in Tidy dodecahedra and icosahedra. Precursor: Explained in Icosahedral precursors. Du Val symbol: As used in The fifty-nine icosahedra and briefly explained here.
3D view
Face diagram
Any further information, including a reference where you can find out more.
2. True lost stellations
The following ten examples are, unarguably, proper stellations of the icosahedron. They were excluded from The 59 because Miller's rules do not understand false vertices or false edges, but treat the parts on either side as separate figures.
| Index Number: | 19 | |
| Precursor: | ||
| Du Val symbol: | Be1 |
 |
 |
Each face is a single 18-gon, connecting ten "cells". The 50 points of contact between the "cells" are all false vertices.
| Index Number: | 39 | |
| Precursor: | ||
| Du Val symbol: | Ce2 |
 |
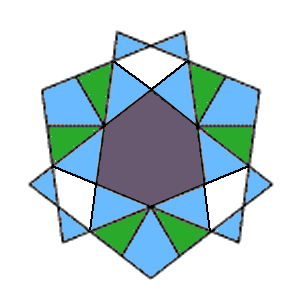 |
This stellation was lost for over 70 years. The model illustrated is preserved in the Department of Pure Mathematics & Mathematical Statistics, at the University of Cambridge, alongside Flather's famous models of the fifty-nine "Miller" icosahedra. It has the gloss finish characteristic of many of H.T. Flather's models, and measures approx. 4 in. (10 cm.) across. Most probably he would have made this model around 1930, before he met Coxeter - who went on to (wrongly) convince him that it is not a proper stellation because it may be divided into inner and outer cell sets. But each face runs across both cell sets, the joining edges between the cells are false, and the figure cannot be divided in two without destroying the structure of every face. The model came to light when Vince Matsko and I visited the Department on 7 July 2006, where I took this photograph.
| Index Number: | 79 | |
| Precursor: | ||
| Du Val symbol: | Df1 |
 |
 |
There are many ways to interpret this face, depending in large part on what you choose to happen in the black interior. The important point is that the "edges" between pink and orange regions are false.
| Index Number: | 257 | |
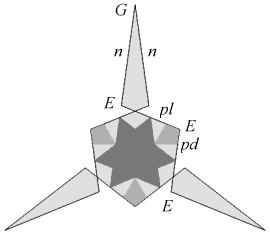
| Precursor: | GnEpdDplEn~EplDmDpd | |
| Du Val symbol: | Af2 |
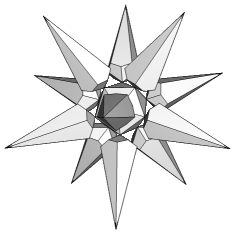 |
 |
Find out more in Icosahedral precursors.
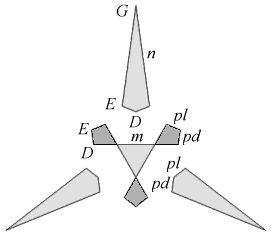
| Index Number: | 271 | |
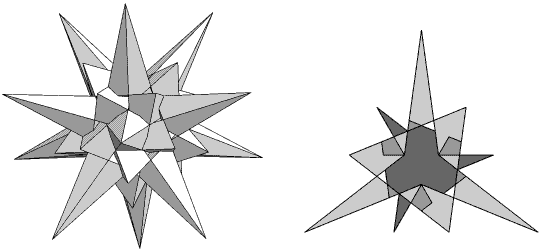
| Precursor: | EpdEplEnGn | |
| Du Val symbol: | Df2 |
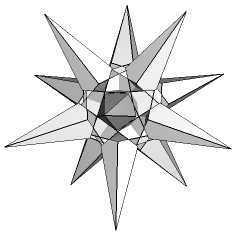 |
 |
Noted by Bridge in 1974, this beautiful polyhedron is a perfect counter-example to the use of Miller's rules in defining stellations. Find out more in Tidy dodecahedra and icosahedra. Bridge did not publish any illustration of it: mine here may well be the first.
| Index Number: | ||
| Precursor: | ||
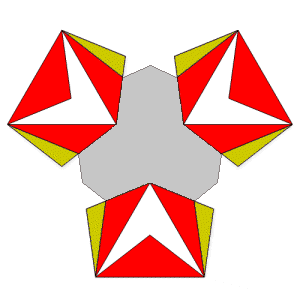
| Du Val symbol: | De1f1f2 |
 |
Find out more in In search of the lost icosahedra.
Other resources: RISC OS (Acorn) Polydata file.
| Index Number: | ||
| Precursor: | ||
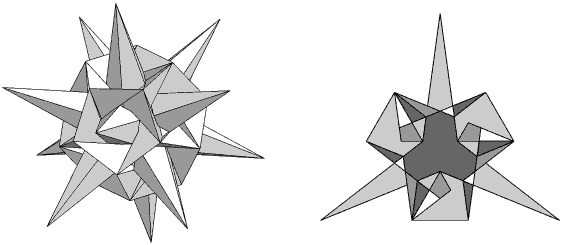
| Du Val symbol: | De1g1 |
 |
 |
The joins between the red and yellow areas in each face are false edges.
Another stellation lost for over 70 years. The model shown here is preserved in the Department of Pure Mathematics & Mathematical Statistics, at the University of Cambridge. It was probably also made by H.T. Flather around 1930 (while this model does not have the glossy finish characteristic of many made by Flather, it is unclear who else might have constructed such a "non-Miller" model).
I rediscovered this stellation on 1st January 2005, but did not come across the Cambridge model until July 2006.
| Index Number: | ||
| Precursor: | ||
| Du Val symbol: | Af2g1 |
 |
 |
Discovered by George "Dinogeorge" Olshevsky in 2004.
The neatest way to interpret each face is as comprising one central dodecagon with three outer hexagons. Other interpretations are possible.
| Index Number: | ||
| Precursor: | ||
| Du Val symbol: | De1f1f2g1 |
 |
Find out more in In search of the lost icosahedra.
Other resources: RISC OS (Acorn) Polydata file.
| Index Number: | ||
| Precursor: | ||
| Du Val symbol: | Af2g2 |
 |
 |
Discovered by George "Dinogeorge" Olshevsky in 2004.
The black areas represent interior regions of face planes, which are are not part of the face. Each face comprises a central enneagon with six outer triangles.
3. Candidate lost stellations
These seven forms may or may not be acceptable as distinct stellations for a variety of reasons, depending on how you define the terms "polyhedron", "stellation", and "distinct". This is not as easy for complicated forms as it is for the simpler ones. Bridge (1974) identifies several figures having the same external forms as certain Miller stellations but differing in internal structure; two examples are included here.
| Index Number: | 35 | |
| Precursor: | BnEpdEplEn ... or not? | |
| Du Val symbol: | be2 |
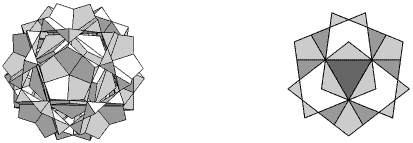 |
The faces have holes in. Are the corners of the holes true or false vertices? Find out more in In search of the lost icosahedra.
Other resources: RISC OS (Acorn) Polydata file.
| Index Number: | 303 | |
| Precursor: | BnGn | |
| Du Val symbol: | De2f2 |
 |
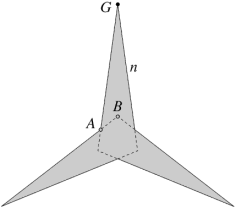 |
Noted by Bridge in 1974, this stellation has the same outer form and Index No. as the De2f2 in The 59, but a different precursor and internal structure (in the face diagram, vertices A are false). The dual facettings of the dodecahedron are properly significant and distinct, so does this mean that the similar-looking stellations are too? Find out more about this and others having the same characteristic in Tidy dodecahedra and icosahedra.
| Index Number: | ||
| Precursor: | ||
| Du Val symbol: | e1g1 |
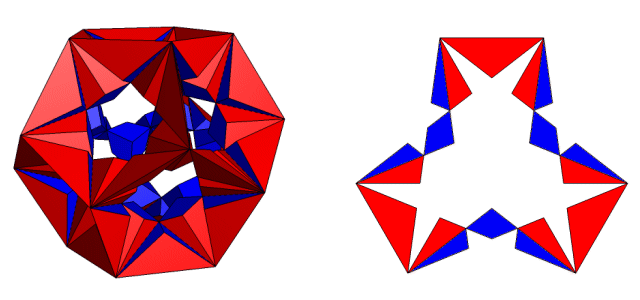 |
The joins between the red and blue areas in each face are false edges. But can a hollow figure such as this be obtained by "extending the faces of the original figure"?. If not, then this figure is not a true stellation - and nor are many "Miller stellations" either.
Discovered by me on 1st January 2005.
| Index Number: | ||
| Precursor: | FmFq | |
| Du Val symbol: | Ef1g1 |
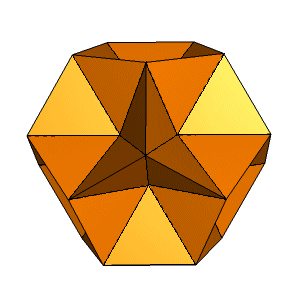 |
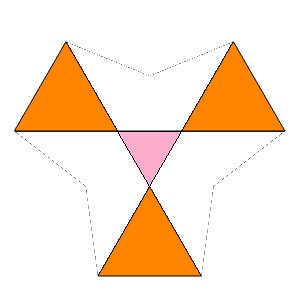 |
Bridge (1974) describes four structural variants having the same outer form, all non-Miller. This is the self-dual one. Branko Grünbaum tells me that it was first described by Theodore Hugel, and illustrated by a pair of stereoscopic diagrams, in a booklet "Die Regulären und Halbregulären Polyeder" (Gottschick-Witter, Neustadt a.d.H., 1876).
Bridge realised that it has a hollow centre, as did Brückner before him. That is to say, the central icosahedron has density 0. One might say that this hollow is technically on the "outside" of the surface, though not all theorists would agree. This distinguishes it as a different polyhedron from the equivalent Miller solid, which has no internal cavity. This internal cavity makes it a distinct stellation.
| Index Number: | ||
| Precursor: | ||
| Du Val symbol: | Cf2g1 |
 |
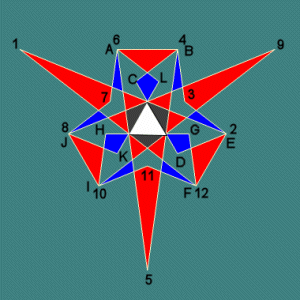 |
Discovered by George "Dinogeorge" Olshevsky in 2004.
A similar issue over false vertices.
| Index Number: | 781 | |
| Precursor: | Several possible | |
| Du Val symbol: | acdf2g1 |
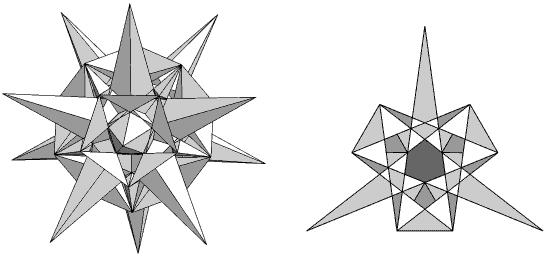 |
The faces have holes in. as for No. 35 above. Find out more in In search of the lost icosahedra.
Other resources: RISC OS (Acorn) Polydata file.
| Index Number: | ||
| Precursor: | CpdKn~KplCn and CplKn~KpdCn | |
| Du Val symbol: | Hj2 |
 |
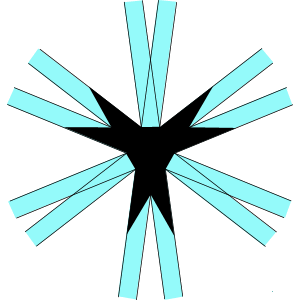 |
My first images of the infinite stellations that are dual to the two compounds of five hemi facetted cubes, as described in Tidy dodecahedra and icosahedra. Each stellation is dual to a different arrangement of the hemi facetted cubes. They both both have the same external appearance, of 30 infinite rhombic prisms, after the manner of the hemi duals in Wenninger's Dual Models. They differ only in the internal arrangement of true and false vertices. But is Wenninger's approach valid?
From the printout lists
Many years ago I wrote a program to produce Stellation Lists under Different Rules, changing the constraints imposed by Miller on The Fifty-Nine Icosdahedra. In particular, I tried getting rid of his Rule (v), which forbad concentric shells of distinct solids. In its place I imposed the weaker conditions that the faces and/or edges must be continuous, i.e. there must be only one connected face in any plane and only one connected edge on any line. Here are the new stellations which the exercise identified. In no way should this list be seen as exhaustive of the lost stellations, the program was just an experiment to try and throw up something - and it did.
Continuous faces in place of rule (v)
36 icosahedra found, of which two are new:
Index DuVal Symbol ----- ------------ 351 D,e1,f1d,f2 863 D,e1,f1d,f2,g1
Continuous edges in place of rule (v)
50 icosahedra found, of which 25 are new:
Index DuVal Symbol
----- ------------
1 33 A,e2
2 35 B,e2
3 39 C,e2
4 103 C,e2,f1d
5 289 A,e2,f2
6 291 B,e2,f2
7 295 C,e2,f2
8 335 D,f1d,f2
9 343 C,e1,f1d,f2
10 351 D,e1,f1d,f2
11 359 C,e2,f1d,f2
12 551 C,e2,g1
13 559 D,e2,g1
14 575 E,g1
15 615 C,e2,f1d,g1
16 783 D,f2,g1
17 791 C,e1,f2,g1
18 799 D,e1,f2,g1
19 807 C,e2,f2,g1
20 815 D,e2,f2,g1
21 831 E,f2,g1
22 847 D,f1d,f2,g1
23 855 C,e1,f1d,f2,g1
24 863 D,e1,f1d,f2,g1
25 871 C,e2,f1d,f2,g1
This list includes both those found above by constraining faces instead of edges. There is also some overlap between the stellations in this list and the various others identified on this page, for example Flather's Ce2 is listed.